The order of performing mathematical operations. Order of actions - Knowledge Hypermarket How to arrange actions

To correctly evaluate expressions in which more than one operation must be performed, you need to know the order in which arithmetic operations are performed. Arithmetic operations in expressions without brackets are agreed to be performed in the following order:

1. If an expression contains exponentiation, then this action is performed first in the order it follows, i.e., from left to right.
2. Then (if present in the expression) the multiplication and division operations are performed in the order they appear.
3. The last operations (if present in the expression) are the addition and subtraction operations in the order in which they appear.

As an example, consider the following expression:

First you need to perform exponentiation (square the number 4 and cube the number 2):

3 16 - 8: 2 + 20

Then multiplication and division are performed (3 multiplied by 16 and 8 divided by 2):

And at the very end, subtraction and addition are performed (subtract 4 from 48 and add 20 to the result):

48 - 4 + 20 = 44 + 20 = 64

Actions of the first and second stages

Arithmetic operations are divided into first and second stage operations. Addition and subtraction are called first stage actions, multiplication and division - second stage actions.

If an expression contains actions of only one step and there are no parentheses in it, then the actions are performed in the order they appear from left to right.

Example 1.

15 + 17 - 20 + 8 - 12

Solution. This expression contains the actions of only one stage - the first (addition and subtraction). It is necessary to determine the order of actions and carry them out.

Answer: 42.

If the expression contains actions of both stages, then the actions of the second stage are executed first, in the order they appear (from left to right), and then the actions of the first stage.

Example. Calculate the value of an expression:

24: 3 + 5 2 - 17

Solution. This expression contains four actions: two of the first stage and two of the second. Let's determine the order in which they are performed: according to the rule, the first action will be division, the second will be multiplication, the third will be addition, and the fourth will be subtraction.

Now let's start the calculation.

And the division of numbers is by actions of the second stage.
The order of actions when finding the values ​​of expressions is determined by the following rules:

1. If there are no parentheses in the expression and it contains actions of only one stage, then they are performed in order from left to right.
2. If the expression contains actions of the first and second stages and there are no parentheses in it, then the actions of the second stage are performed first, then the actions of the first stage.
3. If there are parentheses in the expression, then perform the actions in the parentheses first (taking into account rules 1 and 2).

Example 1. Let's find the value of the expression

a) x + 20 = 37;
b) y + 37 = 20;
c) a - 37 = 20;
d) 20 - m = 37;
e) 37 - s = 20;
e) 20 + k = 0.

636. When subtracting what natural numbers can you get 12? How many pairs of such numbers? Answer the same questions for multiplication and division.

637. Three numbers are given: the first is a three-digit number, the second is the quotient of a six-digit number divided by ten, and the third is 5921. Is it possible to indicate the largest and smallest of these numbers?

638. Simplify the expression:

a) 2a + 612 + 1a + 324;
b) 12у + 29у + 781 + 219;

639. Solve the equation:

a) 8x - 7x + 10 = 12;
b) 13y + 15y- 24 = 60;
c) Зz - 2z + 15 = 32;
d) 6t + 5t - 33 = 0;
e) (x + 59) : 42 = 86;
e) 528: k - 24 = 64;
g) p: 38 - 76 = 38;
h) 43m- 215 = 473;
i) 89n + 68 = 9057;
j) 5905 - 21 v = 316;
k) 34s - 68 = 68;
m) 54b - 28 = 26.

640. A livestock farm provides a weight gain of 750 g per animal per day. What gain does the complex receive in 30 days for 800 animals?

641. There are 130 liters of milk in two large and five small cans. How much milk does a small can contain if its capacity is four times less than the capacity of a larger one?

642. The dog saw its owner when it was 450 m away from him and ran towards him at a speed of 15 m/s. What will be the distance between the owner and the dog in 4 s; after 10 s; in t s?

643. Solve the problem using the equation:

1) Mikhail has 2 times more nuts than Nikolai, and Petya has 3 times more than Nikolai. How many nuts does each person have if everyone has 72 nuts?

2) Three girls collected 35 shells on the seashore. Galya found 4 times more than Masha, and Lena found 2 times more than Masha. How many shells did each girl find?

644. Write a program to evaluate the expression

8217 + 2138 (6906 - 6841) : 5 - 7064.

Write this program in diagram form. Find the meaning of the expression.

645. Write an expression using the following calculation program:

1. Multiply 271 by 49.
2. Divide 1001 by 13.
3. Multiply the result of command 2 by 24.
4. Add the results of commands 1 and 3.

Find the meaning of this expression.

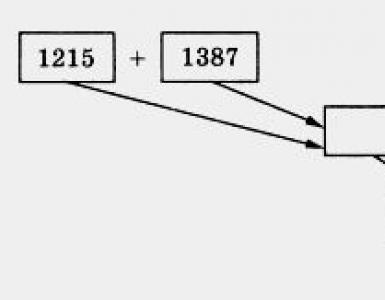
646. Write an expression according to the diagram (Fig. 60). Write a program to calculate it and find its value.

647. Solve the equation:

a) Zx + bx + 96 = 1568;
b) 357z - 1492 - 1843 - 11 469;
c) 2y + 7y + 78 = 1581;
d) 256m - 147m - 1871 - 63,747;
e) 88 880: 110 + x = 809;
f) 6871 + p: 121 = 7000;
g) 3810 + 1206: y = 3877;
h) k + 12 705: 121 = 105.

648. Find the quotient:

a) 1,989,680: 187; c) 9 018 009: 1001;
b) 572 163: 709; d) 533,368,000: 83,600.

649. The motor ship traveled along the lake for 3 hours at a speed of 23 km/h, and then along the river for 4 hours. How many kilometers did the ship travel in these 7 hours if it moved along the river 3 km/h faster than along the lake?

650. Now the distance between the dog and the cat is 30 m. In how many seconds will the dog catch up with the cat if the dog’s speed is 10 m/s, and the cat’s is 7 m/s?

651. Find in the table (Fig. 61) all the numbers in order from 2 to 50. It is useful to perform this exercise several times; You can compete with a friend: who can find all the numbers faster?

N.Ya. VILENKIN, V. I. ZHOKHOV, A. S. CHESNOKOV, S. I. SHVARTSBURD, Mathematics grade 5, Textbook for general education institutions

Lesson plans for 5th grade mathematics download, textbooks and books for free, development of mathematics lessons online

Lesson content lesson notes supporting frame lesson presentation acceleration methods interactive technologies Practice tasks and exercises self-test workshops, trainings, cases, quests homework discussion questions rhetorical questions from students Illustrations audio, video clips and multimedia photographs, pictures, graphics, tables, diagrams, humor, anecdotes, jokes, comics, parables, sayings, crosswords, quotes Add-ons abstracts articles tricks for the curious cribs textbooks basic and additional dictionary of terms other Improving textbooks and lessonscorrecting errors in the textbook updating a fragment in a textbook, elements of innovation in the lesson, replacing outdated knowledge with new ones Only for teachers perfect lessons calendar plan for the year; methodological recommendations; discussion program Integrated Lessons

Rules for the order of performing actions in complex expressions are studied in 2nd grade, but children practically use some of them in 1st grade.

First, we consider the rule about the order of operations in expressions without parentheses, when numbers are performed either only addition and subtraction, or only multiplication and division. The need to introduce expressions containing two or more arithmetic operations of the same level arises when students become familiar with the computational techniques of addition and subtraction within 10, namely:

Similarly: 6 - 1 - 1, 6 - 2 - 1, 6 - 2 - 2.

Since to find the meanings of these expressions, schoolchildren turn to objective actions that are performed in a certain order, they easily learn the fact that arithmetic operations (addition and subtraction) that take place in expressions are performed sequentially from left to right.

Students will first encounter number expressions containing addition and subtraction operations and parentheses in the topic "Addition and Subtraction within 10." When children encounter such expressions in 1st grade, for example: 7 - 2 + 4, 9 - 3 - 1, 4 +3 - 2; in 2nd grade, for example: 70 - 36 +10, 80 - 10 - 15, 32+18 - 17; 4*10:5, 60:10*3, 36:9*3, the teacher shows how to read and write such expressions and how to find their meaning (for example, 4*10:5 read: 4 multiply by 10 and divide the resulting result at 5). By the time they study the topic “Order of Actions” in 2nd grade, students are able to find the meanings of expressions of this type. The goal of the work at this stage is to rely on the practical skills of students, to draw their attention to the order of performing actions in such expressions and to formulate the corresponding rule. Students independently solve examples selected by the teacher and explain in what order they performed them; actions in each example. Then they formulate the conclusion themselves or read from a textbook: if in an expression without parentheses only the actions of addition and subtraction (or only the actions of multiplication and division) are indicated, then they are performed in the order in which they are written (i.e., from left to right).

Despite the fact that in expressions of the form a+b+c, a+(b+c) and (a+b)+c the presence of parentheses does not affect the order of actions due to the associative law of addition, at this stage it is more advisable to orient students to that the action in parentheses is performed first. This is due to the fact that for expressions of the form a - (b + c) and a - (b - c) such a generalization is unacceptable and it will be quite difficult for students at the initial stage to navigate the assignment of brackets for various numerical expressions. The use of parentheses in numerical expressions containing addition and subtraction operations is further developed, which is associated with the study of such rules as adding a sum to a number, a number to a sum, subtracting a sum from a number and a number from a sum. But when first introducing parentheses, it is important to direct students to do the action in the parentheses first.

The teacher draws the children's attention to how important it is to follow this rule when making calculations, otherwise you may get an incorrect equality. For example, students explain how the meanings of the expressions are obtained: 70 - 36 +10 = 24, 60:10 - 3 = 2, why they are incorrect, what meanings these expressions actually have. Similarly, they study the order of actions in expressions with brackets of the form: 65 - (26 - 14), 50: (30 - 20), 90: (2 * 5). Students are also familiar with such expressions and can read, write and calculate their meaning. Having explained the order of actions in several such expressions, children formulate a conclusion: in expressions with brackets, the first action is performed on the numbers written in brackets. Examining these expressions, it is not difficult to show that the actions in them are not performed in the order in which they are written; to show a different order of their execution, and parentheses are used.

The following introduces the rule for the order of execution of actions in expressions without parentheses, when they contain actions of the first and second stages. Since the rules of procedure are accepted by agreement, the teacher communicates them to the children or the students learn them from the textbook. In order for students to understand the introduced rules, along with training exercises, they include solving examples with an explanation of the order of their actions. Exercises in explaining errors in the order of actions are also effective. For example, from the given pairs of examples, it is proposed to write down only those where the calculations were performed according to the rules of the order of actions:

After explaining the errors, you can give a task: using parentheses, change the order of actions so that the expression has the specified value. For example, in order for the first of the given expressions to have a value equal to 10, you need to write it like this: (20+30):5=10.

Exercises on calculating the value of an expression are especially useful when the student has to apply all the rules he has learned. For example, the expression 36:6+3*2 is written on the board or in notebooks. Students calculate its value. Then, according to the teacher’s instructions, the children use parentheses to change the order of actions in the expression:

• 36:6+3-2
• 36:(6+3-2)
• 36:(6+3)-2
• (36:6+3)-2

An interesting, but more difficult, exercise is the reverse exercise: placing parentheses so that the expression has the given value:

• 72-24:6+2=66
• 72-24:6+2=6
• 72-24:6+2=10
• 72-24:6+2=69

Also interesting are the following exercises:

• 1. Arrange the brackets so that the equalities are true:
• 25-17:4=2 3*6-4=6
• 24:8-2=4
• 2. Place “+” or “-” signs instead of asterisks so that you get the correct equalities:
• 38*3*7=34
• 38*3*7=28
• 38*3*7=42
• 38*3*7=48
• 3. Place arithmetic signs instead of asterisks so that the equalities are true:
• 12*6*2=4
• 12*6*2=70
• 12*6*2=24
• 12*6*2=9
• 12*6*2=0

By performing such exercises, students become convinced that the meaning of an expression can change if the order of actions is changed.

To master the rules of the order of actions, it is necessary in grades 3 and 4 to include increasingly complex expressions, when calculating the values ​​of which the student would apply not one, but two or three rules of the order of actions each time, for example:

• 90*8- (240+170)+190,
• 469148-148*9+(30 100 - 26909).

In this case, the numbers should be selected so that they allow actions to be performed in any order, which creates conditions for the conscious application of the learned rules.

Methodological approaches to studying the rules for the order of actions in expressions in primary school

Fedorova Ekaterina Borisovna

primary school teacher at Municipal Educational Institution “Secondary School No. 8”, Nizhnevartovsk

Among the skills that students graduating from primary school must master, the program indicates the ability to calculate the value of numerical expressions containing two to three actions. But practice shows that students make mistakes in the order of performing actions in expressions. Especially in expressions, for example, containing actions of different stages in brackets. This is also observed in the 5th grade, where the number of actions in expressions increases significantly, and the structure of a numerical expression becomes more complex compared to the 4th grade.

Let's consider the sequence of studying expressions in the initial course of mathematics in the approach of M.I. Moro. Children encounter the simplest numerical expressions (sum of the form 2+3, difference of the form 5-1) starting from the first steps in learning arithmetic operations. The most important thing is for children to understand that when solving a problem like: “There are 2 apples on one plate, 5 apples on the other. How many apples are there on these plates? “- you can answer the question posed not only by saying that there are only 7 apples on them, but also like this: “In total there are 2 + 5 apples on these plates.” When continuing the task: “They ate three apples,” children make up a numerical expression in two steps: 2+5-3. At the same time, answering the question: “How many apples are left?”, first-graders learn to distinguish between the concepts of “expression” and “meaning.” expressions." Every number is also considered as an expression. You can create new expressions from expressions by connecting them with arithmetic symbols. In order to indicate which expressions are connected, it becomes necessary to use additional symbols - parentheses. To find the value of an expression, it is important to know the rules for the order of actions in expressions.

Preparation for learning such rules begins in first grade. On a practical level, when first graders learn to add or subtract two numbers in sequence, for example: 6+2+1, 7-1-3, children learn the order of operations in such expressions. They reason: “First you need to add 2 to 6, you get 8. If you add 1 to 8, you get 9.” In 2nd grade, students learn the rule:actions in brackets are performed first.We are considering a task of the form: From the number 10, subtract the sum of the numbers 6 and 3. The teacher explains to emphasize that the sum of the numbers must be subtracted immediately.

10 - 6+3=1, circle the sum in an oval. Remove the excess part of the oval so that the entry fits on the line. The remaining part of the oval is called brackets: 10-(6+3)=1. A formula is formed.

The order of performing actions in expressions is studied in 3rd grade, when three rules are introduced: for expressions without brackets with actions of the same level, for expressions without brackets with actions of different levels, and for expressions with brackets. Each rule can be represented as a model. Slide

Features of Numerical Expression

No.	Peculiarities numerical expressions	Order execution actions	Model
	Contains only + or – or only x or:	In order (from left to right)
	Contains not only + and - , but also x or:	First, perform in order (from left to right) x and:, and then + and – (from left to right)
	Contains one or more pairs of parentheses	First, find the values ​​of the expressions in parentheses, and then perform actions according to rules 1 and 2

The third rule is conveniently presented in algorithmic form.

When finding the value of an expression, actions are performed in the following order:

1) actions written in brackets;

2) multiplication and division actions, in order from left to right;

3) actions, addition and subtraction, in order from left to right.

It is useful to illustrate the rules clearly.

Expressions of a complex expression structure can contain several pairs of brackets, then the rules for the order of actions in the expressions can be represented by the following model: the most complex expressions in brackets contain all four actions. It is convenient to represent the order of actions in them using the following model:

Let's consider N.B. Istomina's approach to studying the rules for the order of actions in expressions. In the manual N.B. Istomina Mathematics: program for grades 1-4, the formation of educational actions is clearly expressed, this is carried out in the textbook when studying all sections of the initial mathematics course. This includes the “Expressions” section. In the "Arithmetic Operations" section, the topic "Numerical Expressions" is found. In first grade, when studying the topic “Addition,” students are introduced to the concept of “mathematical expressions.”

In third grade, the topic “Rules for the order of actions in expressions” is studied. Next, the topic “Similarities and differences of numerical expressions”, “Transformation of numerical expressions” is considered.

N.B. Istomina’s textbooks present an interesting system of educational tasks on the application of rules for the order of actions in expressions. For example:

1. When solving a problem, students make up expressions. They discuss, prove and realize that the “()” sign is important. For example, 39-1·6+3·5, 39-(1·6+3·5).

2. Arrange the order of actions in each diagram and explain which rule for the order of actions in expressions you used:

□-□·(□+□)+□:□-□

(□-□):□-□·(□+□)+□

3.What arithmetic operations can be performed in the specified order?

4.What numbers can be inserted into the “windows” to obtain correct equalities:

□-□·□+□=72

(□-□)□·□+□=100

The correct application of the rules for the order of actions is significantly influenced by the structure of expressions and numerical material. In the structure of expressions, a large role is played by the set, number and location of actions in expressions, and the presence of parentheses in them. Let us characterize some of them. In expressions containing both actions of the same level, the errors are that students give priority to addition before subtraction and multiplication before division, without paying attention to the order in which they are written. For example: In the expression 70:5*2 = 7, the child performs the action first - multiplication, and the second - division. One of the reasons for such errors is the peculiarity of students’ perception and reproduction of the corresponding rules for the order of performing actions. Another reason for these errors is that students are focused not on the rules, but on the ability to perform actions - that is, on numerical material. To eliminate such errors, it is useful to work with expression models, where numbers are indicated by “boxes” and actions are indicated. It is necessary to determine the order of their execution.

In an expression with three actions, students more often make mistakes in the order of performing actions than in expressions with two actions, in which only one action must be chosen and to which only one rule for the order of actions can be applied. For example, when calculating the values ​​of the expression 90-48+12:6, there are significantly more errors than when calculating the value of the expression 80-43+17. Therefore, based on the fact that students are able to apply the rule of order of actions, it cannot be said that they will be able to apply it just as successfully in expressions with three or four actions. This is especially evident in expressions with brackets. All students perform the action in brackets first, so in expressions containing only two actions there are no errors in the order of actions. On the contrary, in expressions with three actions with brackets there are many errors: 100-(44-24):4=20, that is, the guys make mistakes, claiming that they first perform the action in brackets, and then the rest of the actions in the order they are written.

Thus, the central role in the process of developing knowledge and skills belongs to a system of exercises, including educational tasks with constant complication:

Calculate the value of the expression;

Selection of expressions according to their structural characteristics;

Compare expressions and the order in which actions are performed in them;

Find and explain errors

More difficult is changing expressions and the order of actions, completing expressions and, finally, constructing expressions taking into account one or more conditions.

Bibliography

1. Ivashova O.A. Errors in the order of performing arithmetic operations and ways to prevent them // Primary school. – 1988. – No. 4. – P. 26-30.
2. Moro M.I. and Pyshkalo A.M. Methods of teaching mathematics in grades I – III. Teacher's manual. – M.: “Enlightenment”, 1978. – p.336.
3. Shadrina I.V. On the order of actions in an arithmetic expression // Elementary school. – 2000. – No. 2. – pp. 105-107.

When we work with various expressions that include numbers, letters and variables, we have to perform a large number of arithmetic operations. When we do a conversion or calculate a value, it is very important to follow the correct order of these actions. In other words, arithmetic operations have their own special order of execution.

Yandex.RTB R-A-339285-1

In this article we will tell you which actions should be done first and which ones after. First, let's look at a few simple expressions that contain only variables or numeric values, as well as division, multiplication, subtraction and addition signs. Then let's take examples with parentheses and consider in what order they should be calculated. In the third part we will give the necessary order of transformations and calculations in those examples that include signs of roots, powers and other functions.

Definition 1

In the case of expressions without parentheses, the order of actions is determined unambiguously:

1. All actions are performed from left to right.
2. We perform division and multiplication first, and subtraction and addition second.

The meaning of these rules is easy to understand. The traditional left-to-right writing order defines the basic sequence of calculations, and the need to multiply or divide first is explained by the very essence of these operations.

Let's take a few tasks for clarity. We used only the simplest numerical expressions so that all calculations could be done mentally. This way you can quickly remember the desired order and quickly check the results.

Example 1

Condition: calculate how much it will be 7 − 3 + 6 .

Solution

There are no parentheses in our expression, there is also no multiplication and division, so we perform all the actions in the specified order. First we subtract three from seven, then add six to the remainder and end up with ten. Here is a transcript of the entire solution:

7 − 3 + 6 = 4 + 6 = 10

Answer: 7 − 3 + 6 = 10 .

Example 2

Condition: in what order should the calculations be performed in the expression? 6:2 8:3?

Solution

To answer this question, let’s reread the rule for expressions without parentheses that we formulated earlier. We only have multiplication and division here, which means we keep the written order of calculations and count sequentially from left to right.

Answer: First we divide six by two, multiply the result by eight and divide the resulting number by three.

Example 3

Condition: calculate how much it will be 17 − 5 · 6: 3 − 2 + 4: 2.

Solution

First, let's determine the correct order of operations, since we have all the basic types of arithmetic operations here - addition, subtraction, multiplication, division. The first thing we need to do is divide and multiply. These actions do not have priority over each other, so we perform them in the written order from right to left. That is, 5 must be multiplied by 6 to get 30, then 30 divided by 3 to get 10. After that, divide 4 by 2, this is 2. Let's substitute the found values ​​into the original expression:

17 − 5 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

There is no longer division or multiplication here, so we do the remaining calculations in order and get the answer:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Answer:17 − 5 6: 3 − 2 + 4: 2 = 7.

Until the order of performing actions is firmly memorized, you can put numbers above the signs of arithmetic operations indicating the order of calculation. For example, for the problem above we could write it like this:

If we have letter expressions, then we do the same with them: first we multiply and divide, then we add and subtract.

What are the first and second stage actions?

Sometimes in reference books all arithmetic operations are divided into actions of the first and second stages. Let us formulate the necessary definition.

The operations of the first stage include subtraction and addition, the second - multiplication and division.

Knowing these names, we can write the previously given rule regarding the order of actions as follows:

Definition 2

In an expression that does not contain parentheses, you must first perform the actions of the second stage in the direction from left to right, then the actions of the first stage (in the same direction).

Order of calculations in expressions with parentheses

The parentheses themselves are a sign that tells us the desired order of actions. In this case, the required rule can be written as follows:

Definition 3

If there are parentheses in the expression, then the first step is to perform the operation in them, after which we multiply and divide, and then add and subtract from left to right.

As for the parenthetical expression itself, it can be considered as an integral part of the main expression. When calculating the value of the expression in brackets, we maintain the same procedure known to us. Let's illustrate our idea with an example.

Example 4

Condition: calculate how much it will be 5 + (7 − 2 3) (6 − 4) : 2.

Solution

There are parentheses in this expression, so let's start with them. First of all, let's calculate how much 7 − 2 · 3 will be. Here we need to multiply 2 by 3 and subtract the result from 7:

7 − 2 3 = 7 − 6 = 1

We calculate the result in the second brackets. There we have only one action: 6 − 4 = 2 .

Now we need to substitute the resulting values ​​into the original expression:

5 + (7 − 2 3) (6 − 4) : 2 = 5 + 1 2: 2

Let's start with multiplication and division, then perform subtraction and get:

5 + 1 2: 2 = 5 + 2: 2 = 5 + 1 = 6

This concludes the calculations.

Answer: 5 + (7 − 2 3) (6 − 4) : 2 = 6.

Don't be alarmed if our condition contains an expression in which some parentheses enclose others. We only need to apply the rule above consistently to all expressions in parentheses. Let's take this problem.

Example 5

Condition: calculate how much it will be 4 + (3 + 1 + 4 (2 + 3)).

Solution

We have parentheses within parentheses. We start with 3 + 1 + 4 · (2 ​​+ 3), namely 2 + 3. It will be 5. The value will need to be substituted into the expression and calculated that 3 + 1 + 4 · 5. We remember that we first need to multiply and then add: 3 + 1 + 4 5 = 3 + 1 + 20 = 24. Substituting the found values ​​into the original expression, we calculate the answer: 4 + 24 = 28 .

Answer: 4 + (3 + 1 + 4 · (2 ​​+ 3)) = 28.

In other words, when calculating the value of an expression that includes parentheses within parentheses, we start with the inner parentheses and work our way to the outer ones.

Let's say we need to find how much (4 + (4 + (4 − 6: 2)) − 1) − 1 will be. We start with the expression in the inner brackets. Since 4 − 6: 2 = 4 − 3 = 1, the original expression can be written as (4 + (4 + 1) − 1) − 1. Looking again at the inner parentheses: 4 + 1 = 5. We have come to the expression (4 + 5 − 1) − 1 . We count 4 + 5 − 1 = 8 and as a result we get the difference 8 - 1, the result of which will be 7.

The order of calculation in expressions with powers, roots, logarithms and other functions

If our condition contains an expression with a power, root, logarithm or trigonometric function (sine, cosine, tangent and cotangent) or other functions, then first of all we calculate the value of the function. After this, we act according to the rules specified in the previous paragraphs. In other words, functions are equal in importance to the expression enclosed in brackets.

Let's look at an example of such a calculation.

Example 6

Condition: find how much is (3 + 1) · 2 + 6 2: 3 − 7.

Solution

We have an expression with a degree, the value of which must be found first. We count: 6 2 = 36. Now let’s substitute the result into the expression, after which it will take the form (3 + 1) · 2 + 36: 3 − 7.

(3 + 1) 2 + 36: 3 − 7 = 4 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Answer: (3 + 1) 2 + 6 2: 3 − 7 = 13.

In a separate article devoted to calculating the values ​​of expressions, we provide other, more complex examples of calculations in the case of expressions with roots, degrees, etc. We recommend that you familiarize yourself with it.

If you notice an error in the text, please highlight it and press Ctrl+Enter