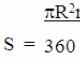Metric spaces. Metrics. Examples. Compressed mappings Examples of metric spaces with proof

metric space.

metric space is a set in which the distance between any pair of elements is defined.

A metric space is a pair , where is a set ( subject set metric space, set points metric space), and is a numerical function ( metrics space), which is defined on the Cartesian product and takes values in the set of real numbers - such that for points

Note: It follows from the axioms that the distance function is non-negative, since

Compressed displays.

Compressed mappings one of the main provisions of the theory metric spaces on the existence and uniqueness of a fixed point of a set under some special (“contracting”) mapping of it into itself. S. o. p. are used mainly in the theory of differential and integral equations.

Arbitrary display A metric space M into itself, which to each point X from M matches some point y = ax from M, generates in space M the equation

Ax = x. (*)

Display action A point X can be interpreted as moving it to a point y = ax. Dot X is called the fixed point of the mapping A if equality (*) holds. That. the question of the solvability of the equation (*) is the question of finding the fixed points of the map A.

Display A metric space M into itself is called contracted if there exists such a positive number a< 1, что для любых точек X And at from M the inequality

d( Ax, ay) £ a d(x, y),

where symbol d(u, u) means distance between points u and u of the metric space M.

S. o. asserts that every contracted mapping of a complete metric space into itself has, and moreover, only one, fixed point. Moreover, for any starting point x0 from M subsequence ( x n) determined by the recurrence relations

x n \u003d Ax n-1, n = 1,2,...,

has a fixed point as its limit X display A. In this case, the following error estimate is valid:

S. o. n. allows one to prove important theorems on the existence and uniqueness of solutions to differential, integral, and other equations by a unified method. Under the conditions of applicability of S. o. n. the solution can be calculated with a predetermined accuracy successive approximations by the method.

With the help of a certain choice of the complete metric space M and display construction A these problems are first reduced to the equation (*), and then they find the conditions under which the mapping A appears to be compressed.

The convergence of mappings with respect to this metric is equivalent to their uniform convergence on the entire space .

In the particular case when is a compact space and is a real line, one obtains the space of all continuous functions on the space X with the metric of uniform convergence.

In order for this function to become a metric, in the first two spaces it is necessary to identify functions that differ on a set of measure 0. Otherwise, this function will be just a semimetric. (In the space of functions that are continuous on an interval, functions that differ on a set of measure 0 coincide anyway.)

Until now, speaking of distance, we have always meant the Euclidean distance. So, we defined the distance between vectors as the length of the vector, namely:

But distances can be calculated in another way, using different measures of length. For example, consider a simplified map of a city in the form of a rectangular grid of two-way streets. Then an adequate measure of length can be the shortest distance that must be overcome to get from one intersection to another. Sometimes this distance is called Manhattan.

Instead of listing all kinds of measures of length, most of which we will not need, we will now consider the requirements (axioms) that an arbitrary measure of length must satisfy. All subsequent distance theorems will be proved within the framework of these axioms, that is, in the most general form. In mathematics, it is customary to use the term metric instead of the expression "measure of length".

Metrics.

A metric on a set X is a real function d(x, y) defined on the product x and satisfying the following axioms:

b) entails

d) for all (triangle inequality).

A pair is called a metric space. The proof that the Euclidean distance satisfies axioms (a), (b), and (c) is trivial. Triangle Inequality:

we proved in § 3.1 (Theorem 3.1.2). Thus, the Euclidean distance is a metric, which we will henceforth call the Euclidean metric.

Consider one important class of metrics in space, namely the class of -metrics. -metric is a generalization of the Euclidean metric and coincides with it for . For the p-metric is defined as follows:

We will leave the following fact without proof:

The proof that the -metric is indeed a metric, i.e. satisfies the axioms we also omit. Partially, this question is included in the exercises.

Note that in the definition of the metric, we did not require that the elements x and y belong to the space . This enables us to define the set X, as well as its elements x, y, etc., in many different ways. Our task is to indicate under what conditions the fractal construction converges. To do this, you need to be able to measure the distance between compact sets, that is, you need to determine the appropriate metric.

Set theory in metric spaces.

We have to take a big step forward and extend the set-theoretic definitions of Section 3.1, which implied the Euclidean metric, to arbitrary metrics. An open ball in a metric space (X, d) is defined as follows:

Taking into account (3.4), we can leave the above definitions of the following concepts unchanged:

For example, a set is an open set if and only if for any it is possible to specify an open ball (in the sense of definition (3.4)), which is contained in E. All definitions are included in the list without changes, except for the concept of compactness. A rigorous definition of a compact set in an arbitrary metric space is given in App. Since we are mainly interested in the compactness of subsets of space, the definition given above (closedness and boundedness) remains valid.

If is a metric on the set X, and is a one-to-one real function, then

there is also a metric on X. Axioms (a) and (c) are obviously satisfied. satisfies axiom (b), since is a one-to-one function. Axiom (d) can be written as an inequality:

that is, the classical triangle inequality for real numbers. An example of a metric defined like this:

Two metrics, defined on a set X, are said to be equivalent if one can specify such that:

It can be shown that any two -metrics in the space where are equivalent (the case is taken out in exercise 3 at the end of this section). On the other hand, the metrics on the set R are not equivalent (Ex. 4 at the end of this section).

Apparently, the main consequence of the equivalence of metrics for the theory of fractals is the fact that the fractal dimension (Chapter 5) is preserved when the metric is replaced by an equivalent one. Moreover, if a set is open (closed) in one metric, then it is also open (closed) in any equivalent metric. Further, if a set is bounded in one metric, then it is bounded in any equivalent metric. The same applies to perfect, connected, and completely discontinuous sets.

Convergence.

Let be a metric on a set X. A sequence of points of a metric space X converges to the limit in the metric d if the sequence of numbers converges to zero in the usual sense, that is, if:

Here the equivalence of metrics is expressed as follows. If the metrics are equivalent, then in the -metric if and only if in the -metric, since:

If so, and vice versa.

Continuity.

In the course of mathematical analysis, a function defined on X is called continuous at a point if.

One of the most important operations of analysis is the passage to the limit. This operation is based on the fact that the distance from one point to another is defined on the number line. Many fundamental facts of analysis are not connected with the algebraic nature of real numbers (that is, with the fact that they form a field), but are based only on the concept of distance. Generalizing the idea of real numbers as a set in which the distance between elements is introduced, we come to the concept of a metric space - one of the most important concepts of modern mathematics.

metric space called a couple (X, r), consisting of some sets(spaces) X items(points) and distance, i.e., a non-negative real function r(x, y), defined for any X And at from X and subject to the following three axioms:

1) r(x, y)= 0 if and only if X = y,

2) r(x, y) = r(y, x)(axiom of symmetry),

3) r(x, r)≤ r(x, y)+ r(y, r)(triangle axiom).

The metric space itself, that is, the pair (X, p), we will denote, as a rule, by one letter:

R = (X, p).

In cases where misunderstandings are ruled out, we will often denote the metric space by the same symbol as the “stock of points” itself. x.

Let us give examples of metric spaces. Some of these spaces play a very important role in the analysis.

1. Setting for elements of an arbitrary set

we obtain, obviously, a metric space. It can be called the space of isolated points.

2. The set of real numbers with distance

ρ(x, y) = | x - y |

forms a metric space R 1 .

3. The set of ordered collections from P real numbers with distance

called P-dimensional arithmetic Euclidean space Rn.

4. Consider the same set of sets from P real numbers, but the distance is defined in it by the formula

The validity of axioms 1)-3) is obvious here. We denote this metric space by the symbol Rn 1 .

5. Take again the same set as in examples 3 and 4, and determine the distance between its elements by the formula

The validity of axioms 1)-3) is obvious. This is the space that we will designate Rn¥ in many questions of analysis is no less convenient than the Euclidean space Rn.

The last three examples show that sometimes it is really important to have different notations for the metric space itself and for the set of its points, since the same stock of points can be metricized in different ways.

6. Many WITH of all continuous real functions defined on the segment with distance

also forms a metric space. Axioms 1)-3) are verified directly. This space plays a very important role in the analysis. We will denote it with the same symbol WITH, which is the set of points in this space itself.

7. Consider, as in Example 6, the collection of all functions continuous on the interval WITH , but we define the distance differently, namely, we set

We will denote such a metric space WITH 2 and call space of continuous functions with a quadratic metric.

What is a metric? What is it for? Is it a physical field?

The metric in our time is strongly associated with the theory of gravity, thanks to the work of Hilbert and Einstein, together with Grossman. However, in mathematics it was introduced long before that. If I'm not mistaken, among the first who somehow used it explicitly were Riemann and Gauss. First, we will try to understand its role in geometry, and only then we will see how the metric became the main structure of GR, the General Theory of Relativity.

To date, there is a fairly detailed and clear definition of metric spaces of a fairly general form:

In mathematics, a metric space (“equipped with a metric”) is a space in which for any two of its ordered points (that is, one of them is called the first and the other the second), a real number is defined such that it is equal to zero, if and only if , when the points coincide, and the “triangle” inequality is satisfied - for any three points (x, y, z) this number for any pair (x, y) is equal to or less than the sum of these numbers for the other two pairs, (x, z) and (y,z). It also follows from the definition that this number is non-negative and does not change (the metric is symmetric) when the order of points in the pair is changed.

As usual, as soon as something is defined, this definition is expanded and the name is extended to other, similar spaces. So here. For example, strictly formally will not be metric according to the definition given above, since in them, the “metric” number, the interval, can be zero for two different points, and its square can also be a negative real number. However, almost from the very beginning they are included in the family of metric spaces, simply removing the corresponding requirement in the definition by extending the definition.

In addition, the metric can also be defined not for all points in space, but only for infinitely close ones (locally). Such spaces are called Riemannian and are also commonly called metric spaces. Moreover, it was the Riemannian spaces that made the metric so famous and attracting the attention of both mathematicians and physicists, and familiar even to many people who have little connection with these sciences.

Ultimately, here we will discuss the metric in relation to Riemannian spaces, i.e. in a local sense. And even locally indefinite.

A formal mathematical definition and its extensions are the result of understanding and clarifying the concept of a metric. Let's see what this concept grew out of, what properties of the real world it was originally associated with.

All geometry arose from those concepts that were originally formalized by Euclid. So is the metric. In Euclidean geometry (for simplicity and clarity, we will talk about two-dimensional geometry, and therefore about the geometry of a plane), there is a concept of the distance between two points. Very often and now the metric is called exactly the distance. Because for the Euclidean plane, the distance is the metric, and the metric is the distance. And that's how it was conceived in the very beginning. Although, as I will try to show, this applies to the modern concept of metrics only in a very limited sense, with many reservations and conditions.

Distance on the Euclidean plane (on a piece of paper) seems to be an extremely simple and obvious thing. Indeed, using a ruler, you can draw a straight line between any two points and measure its length. The resulting number will be the distance. Taking the third point, you can draw a triangle and make sure that this distance (for any two points on the plane) exactly satisfies the definition given above. Actually, the definition was copied one to one from the properties of the Euclidean distance on the plane. And the word “metric” was originally associated with measurement (with the help of a meter), “metrization” of a plane.

And why was it necessary to measure distances, to carry out this very metrization of the plane? Well, for what distances are measured in real life, everyone probably has their own idea. And in geometry, they really thought about it when they introduced coordinates in order to describe each point of the plane separately and uniquely from the others. The coordinate system on the plane will obviously be more complicated than just the distance between two points. Here is the origin, and the coordinate axes, and the distance (how to do without them?) From the origin to the projections of the point on the axis. Why the coordinate system is needed seems to be clear - it is a continuous grid of lines perpendicular to each other (if the coordinates are Cartesian), completely filling the plane and thus solving the problem of the address of any point on it.

It turns out that the metric is distance and the coordinates are distances. Is there a difference? Entered coordinates. Why then the metric? There is a difference, and a very significant one. The choice of coordinate systems implies a certain freedom. In Cartesian systems, we use straight lines as axes. But we can also use curves, can't we? Can. And all sorts of twisty ones too. Can we measure distance along such lines? Certainly. Measuring distance, length along a line is not related to what line it is. A curved path also has a length and you can place milestones on it. But the metric in Euclidean space is not an arbitrary distance. This is the length of the line connecting two points. Straight. And what is it? Which line is straight and which is curved? In a school course, straight lines are an axiom. We see them and catch the idea. But in general geometry, straight lines (in itself this is a name, a label, nothing more!) can be defined as some special lines among all possible ones connecting two points. Namely, as the shortest, having the smallest length. (And in some cases, for some mathematical spaces, on the contrary, the longest, having the greatest length.) It would seem that we have caught the difference between the metric and an arbitrary distance between two points. It wasn't there. We went down the wrong path. Yes, that's right, straight lines are the shortest lines in Euclidean space. But the metric is not just the length of the shortest path. No. This is her secondary property. In Euclidean space, the metric is not just the distance between two points. The metric is, first of all, the image of the Pythagorean theorem. A theorem that allows you to calculate the distance between two points if you know their coordinates, two other distances. Moreover, it is calculated very specifically, as the square root of the sum of squared coordinate distances. The Euclidean metric is not a linear form of coordinate distances, but a quadratic one! Only the specific properties of the Euclidean plane make the connection of the metric with the shortest paths connecting points so simple. Distances are always linear functions of displacement along the path. The metric is a quadratic function of these displacements. And here lies the fundamental difference between the metric and the intuitively understood distance, as a linear function of displacement from a point. Moreover, for us, in general, the distance is directly associated with the displacement itself.

Why, why on earth is the quadratic function of displacements so important? And does it really have the right to be called distance in the full sense of the word? Or is it a rather specific property of only Euclidean space (well, or some family of spaces close to Euclidean)?

Let's take a small step aside and talk more about the properties of units of measurement. Let's ask ourselves, what should the rulers be in order to be able to draw a coordinate grid on a sheet of paper? Solid, tough and unchanging, you say. And why "lines"? One is enough! True, if it can be rotated arbitrarily in the plane of the paper and transferred along it. Notice the "if"? Yes, we have the opportunity to use such a ruler in relation to the plane. The ruler itself, the plane itself, but the plane allows us to “attach” our ruler to itself. What about a spherical surface? No matter how you apply it, everything sticks out of the surface. I just want to bend it, give up hardness and rigidity. Let's leave this line of thought for now. What more do we want from the line? Hardness and stiffness actually mean something else, much more important for us when measuring - a guarantee of the invariance of the chosen ruler. We want to measure with the same scale. Why is this needed? What do you mean why?! To be able to compare measurement results everywhere in the plane. No matter how we rotate the ruler, no matter how we move it, some of its properties, the length, must be guaranteed to be unchanged. Length is the distance between two points (in a straight line) on a ruler. Very similar to metrics. But the metric is introduced (or exists) in the plane, for the points of the plane, and what does the ruler have to do with it? And despite the fact that metric and is just the image of the constant length of the abstract ruler, taken to its logical conclusion, torn off from the outermost ruler and assigned to each point of the plane.

Although our rulers are always external objects for the distances they measure on the plane, we also think of them as internal scales belonging to the plane. Therefore, we are talking about a common property, both the outer ruler and the inner one. And the property is one of the two main ones - the value, what makes the scale a unit of measurement (the second property of the scale is the direction). For Euclidean space, this property seems to be independent of the direction of the ruler and its position (from a point in space). There are two ways to express this independence. The first way, a passive view of things, speaks of the invariance of a quantity, its identity with an arbitrary choice of acceptable coordinates. The second way, active look, speaks of invariance under displacement and rotation, as a result of an explicit transition from point to point. These methods are not equivalent to each other. The first is simply a formalization of the statement that the value that exists in a given place (point) is the same regardless of the point of view. The second also claims that the values of the quantity at different points are the same. Clearly, this is a much stronger statement.

Let us dwell for the time being on the invariance of the magnitude of the scale for an arbitrary choice of coordinates. Op-pa! Like this? To assign coordinates to points, you already need to have scales. Those. this same line. What are the other coordinates? Other lines? Actually it is! But! The fact that we can rotate our ruler at a point as we like in the Euclidean plane creates the appearance that the coordinates can be changed without changing the ruler. It's an illusion, but such a nice illusion! How we got used to it! We say all the time - a rotated coordinate system. And this illusion is based on some postulated property of the scale in the Euclidean plane - the invariance of its “length” with an arbitrary rotation at a point, i.e. with an arbitrary change in the second property of the scale, direction. And this property takes place at any point of the Euclidean plane. The scale everywhere has a “length” that does not depend on the local choice of the directions of the coordinate axes. This is a postulate for Euclidean space. And how do we determine this length? In a coordinate system in which the selected scale is a unit of measurement along one of the axes, we define it very simply - this is the very unit. And in a coordinate system (rectangular), in which the selected scale does not coincide with any of the axes? Using the Pythagorean theorem. Theorems are theorems, but there is a bit of deception here. In fact, this theorem should replace some of the axioms formulated by Euclid. She is equivalent to them. And with further generalization of geometry (for arbitrary surfaces, for example), they rely precisely on the method of calculating the length of the scale. In fact, they translate this method into the category of axioms.

Let us now repeat something that underlies geometry, which allows us to assign coordinates to points in a plane.

It's about the unit of measurement, the scale. Scale exists at any point. It has a magnitude - "length" and direction. The length is invariant (does not change) when changing direction at a point. In rectangular coordinates in Euclidean space, the square of the length of a scale arbitrarily directed from a point is equal to the sum of the squares of its projections on the axis. Such a geometric quantity is also called a vector. So the scale is a vector. And the “length” of a vector is also called the norm. Fine. But where is the metric? A metrics with this approach, there a way to assign a norm to any vector at each point, a method for calculating this norm for an arbitrary position of this vector relative to the vectors that make up the base, the frame(those that determine the directions of the coordinate axes from a given point and have a unit norm by definition, i.e. units of measurement). It is very important that such a method is defined for each point in space (a plane in this case). Thus, it is a property of this space and its internal vectors, and not objects external to the space.

Excuse me, but already at the very beginning we gave the definition of metric spaces. Why a new definition? And is it consistent with the old? But why. Here we have indicated exactly how it is set, this most real number is determined. Namely, the distance between the points is equal to the “length”, the norm of the vector connecting these points (in Euclidean space). The fact that a vector has some norm, independent of the point of view on it (the choice of a frame) is the definition of a vector. The most important condition, which makes the space metric, is the requirement that vectors with a given norm exist at every point in the space in all directions. And this definition is quite consistent with the one given at the very beginning. Is it possible to define a metric on some space in another way? Basically, you can. And even in many ways. Only these will be completely different classes of spaces that do not include the Euclidean space even as a special case.

Why is the Euclidean space special for us? Well, how is it than? At first glance, it is precisely these properties that the very space in which we live possesses. Yes, upon closer inspection, not exactly the same. But is there a difference between “not quite like that” and “not quite like that”?! Although the set of words seems to be the same. So our space-time, if not Euclidean, then under certain conditions can be very close to it. Therefore, we must choose from the family of spaces in which the Euclidean space exists. That's how we do it. But still, what is so special about Euclidean space that finds its expression in certain properties of its metric? There are quite a lot of properties, most of them have already been mentioned above. I will try to formulate this feature rather compactly. Euclidean space is such that it is possible to choose scales (that is, enter coordinates) in it so that it is completely filled with a rectangular grid of coordinates. Perhaps this is when the metric at each point in space is the same. In essence, this means that the scales needed for this exist at every point in space and they are all identical to one single one. For the whole space, one ruler is enough, which can be transferred to any point (in the active sense) without changing both its size and its direction.

Above, I posed the question why the metric is a quadratic bias function. It remains unanswered so far. We will definitely come to this. And now note for yourself for the future - the metric in the family of spaces we need is a quantity invariant under coordinate transformations. We have been talking about Cartesian coordinates so far, but I will immediately emphasize here that this is true for any coordinate transformations that are valid at a given point in a given space. A quantity that is invariant (not changing) during coordinate transformations has another special name in geometry - scalar. See how many names for the same - constant, invariant, scalar... Maybe there is something else, it doesn’t immediately come to mind. This speaks to the importance of the concept itself. So, the metric is a scalar in a certain sense. Of course, there are other scalars in geometry.

Why in a "certain sense"? Because, the concept of metrics includes two points and not one! A vector is associated (defined) with only one point. So I misled you? No, I just haven't said everything that needs to be said. But it must be said that the metric is not the norm of an arbitrary vector, but only of an infinitesimal displacement vector from a given point in an arbitrary direction. When this norm is independent of the direction of displacement from a point, then its scalar value can be considered as a property of that one point only. At the same time, it still remains the rule for calculating the norm for any other vector. Like this.

Something doesn’t add up ... The norms are different for different vectors! And the metric is a scalar, the value is the same. Contradiction!

There is no contradiction. I said clearly - the rule of calculation. For all vectors. And the specific value itself, which is also called the metric, is calculated according to this rule for only one vector, the displacement. Our language is accustomed to liberties, defaults, abbreviations ... So we are used to calling both a scalar and a rule for its calculation a metric. In fact, it's almost the same thing. Almost, but not quite. It is still important to see the difference between the rule and the result obtained with its help. And what is more important - the rule or the result? Oddly enough, in this case, the rule ... Therefore, much more often in geometry and physics, when they talk about metrics, they mean exactly the rule. Only very stubborn mathematicians prefer to speak strictly about the result. And there are reasons for this, but about them elsewhere.

I also want to note that in a more conventional way of presentation, when the concepts of vector spaces are taken as the basis, the metric is introduced as a dotted pairwise product of all vectors of the basis, the frame. In this case, the scalar product of the vectors must be determined beforehand. And on the path that I followed here, it is the presence of a metric tensor in space that allows us to introduce, define the scalar product of vectors. Here the metric is primary, its presence allows us to introduce the scalar product as a kind of invariant connecting two different vectors. If a scalar for the same vector is calculated using a metric, then this is simply its norm. If this scalar is calculated for two different vectors, then this is their dot product. If this is also the norm of an infinitely small vector, then it is quite acceptable to call it simply the metric at a given point.

And what can we say about the metric as a rule? Here we have to use formulas. Let the coordinates along the axis with number i be denoted as x i . And the offset from the given point to the neighboring one is dx i . I draw your attention - the coordinates are not a vector! And the displacement is just a vector! In such notation, the metric “distance” between a given point and a neighboring one, according to the Pythagorean theorem, will be calculated using the formula

ds 2 = g ik dx i dx k

On the left here is the square of the metric “distance” between the points, the “coordinate” (that is, along each individual coordinate line) distance between which is given by the displacement vector dx i . On the right is the sum over the coinciding indices of all pairwise products of the components of the displacement vector with the corresponding coefficients. And their table, the matrix of coefficients g ik , which sets the rule for calculating the metric norm, is called the metric tensor. And it is this tensor in most cases that is called the metric. The term "" is extremely important here. And it means that in another coordinate system the formula written above will be the same, only the table will contain other (in the general case) coefficients that are calculated in a strictly specified way through these and coordinate transformation coefficients. Euclidean space is characterized by the fact that in Cartesian coordinates the form of this tensor is extremely simple and the same in any Cartesian coordinates. The matrix g ik contains only ones on the diagonal (for i=k), and the rest of the numbers are zeros. If non-Cartesian coordinates are used in Euclidean space, then the matrix in them will not look so simple.

So, we have written down a rule that determines the metric “distance” between two points in Euclidean space. This rule is written for two arbitrarily close points. In Euclidean space, i.e. in one in which the metric tensor can be diagonal with units on the diagonal in some coordinate system at each point, there is no fundamental difference between finite and infinitesimal displacement vectors. But we are more interested in the case of Riemannian spaces (such as the surface of a ball, for example), where this difference is significant. So, we assume that the metric tensor is not generally diagonal and changes as we move from point to point in space. But the result of its application, ds 2 , remains at each point independent of the choice of the direction of displacement and of the point itself. This is a very strict condition (less strict than the Euclidean condition) and it is when it is met that the space is called Riemannian.

You probably noticed that very often I put in quotation marks the words “length” and distance. This is why I do it. In the case of a plane and three-dimensional Euclidean space, the metric "distance" and "length" seem to be exactly the same as the usual distances measured with rulers. Moreover, these concepts were introduced to formalize the work with measurement results. Why, then, “seem to match”? It's funny, but this is exactly the case when mathematicians, along with dirty (not needed by them) water, threw the child out of the bath. No, they left something, but what was left ceased to be a child (distance). This is easy to see even in the example of the Euclidean plane.

Let me remind you that the metric “distance” does not depend on the choice of Cartesian (and not only) coordinates, say, on a sheet of paper. Let in some coordinates, this distance between two points on the coordinate axis is equal to 10. Is it possible to specify other coordinates in which the distance between the same points will be equal to 1? No problem. Just set aside as a unit along the same axes a new unit equal to 10 of the previous ones. Has the Euclidean space changed because of this? What's the matter? But the fact is that when we measure something, it is not enough for us to know the number. We also need to know what units were used to get this number. Mathematics in its usual form is not interested in this. She only deals with numbers. The choice of units of measurement is made before the application of mathematics and should not change anymore! But our distances, lengths, without indicating the scales, do not tell us anything! But math doesn't care. When it comes to metric "distance", its formal application is indifferent to the choice of scale. At least meters, at least fathoms. Only the numbers matter. That's why I put quotes. Do you know what side effect this approach has in the mathematics of Riemannian spaces? But what. Considering the change in scale from point to point does not make sense. Just a change in direction. And this despite the fact that changing the scale with the help of coordinate transformations in such geometry is quite an ordinary thing. Is it possible to include in geometry a consistent consideration of the properties of scales in their entirety? Can. Only to do this, you will have to remove a lot of agreements and learn to call things by their proper, correct names. One of the first steps will be the realization of the fact that no metric is essentially distance and cannot be. It certainly has some physical meaning, and a very important one at that. But different.

In physics, attention to the role of metrics was drawn with the advent of theories of relativity - first special, then general, in which the metric became the central structure of the theory. The Special Theory of Relativity was formed on the basis of the fact that three-dimensional distance is not a scalar from the point of view of a set of inertial, uniformly and rectilinearly moving physical reference frames relative to each other. Another value turned out to be a scalar, an invariant, which was called an interval. The interval between events. And to calculate its value, you need to take into account the time interval between these events. Moreover, it turned out that the rule for calculating the metric (and the interval immediately began to be considered as a metric in the unified space-time, the space of events) is different from the usual Euclidean one in three-dimensional space. Similar, but slightly different. The corresponding metric space of four dimensions introduced by Herman Minkowski, began to be called. It was Minkowski's work that drew the attention of physicists, including Einstein, to the importance of the concept of metric as a physical quantity, not just a mathematical one.

The General Theory of Relativity also included in consideration physical frames of reference accelerated relative to each other. And, thus, she was able to give a description of gravitational phenomena at a new level in relation to Newton's theory. And she was able to achieve this by giving the meaning of the physical field to the metric - both the magnitude and the rule, the metric tensor. At the same time, she uses the mathematical construction of the Riemannian space as an image of space-time. We will not go too far into the details of this theory. Among other things, this theory claims that the world (space-time), in which there are massive bodies, that is, bodies attracted to each other, has a metric different from the Euclidean metric that is so pleasant to us. All statements below are equivalent:

Physical statement. Point bodies that have mass are attracted to each other.

In space-time, in which there are massive bodies, it is impossible to introduce a rigid rectangular grid everywhere. There are no measuring devices that allow you to do this. Always arbitrarily small “cells” of the resulting grid will be curved quadrilaterals.

You can choose a scale with the same value (norm) for the entire space-time. Any such scale can be moved from its point to any other point and compared with the one already existing there. BUT! Even if the offset is infinitely small, the directions of the compared scales will generally not coincide. The stronger, the closer the scale is to a body with mass and the greater this mass. Only where there are no masses (however, here's a question for you - what about the scales themselves?) The directions will coincide.

In the space-time region containing massive bodies, there is no such coordinate system in which the metric tensor at each point is represented by a matrix that is zero everywhere except for the diagonal, on which the units are located.

The difference between the metric and the Euclidean one is a manifestation of the presence of a gravitational field (gravitational field). Moreover, the field of the metric tensor is the gravitational field.

Many more similar statements could be cited, but now I would like to draw your attention to the last one. curvature. This is something we haven't discussed yet. What does it have to do with metrics? For the most part, none! is a more general concept than a metric. In what sense?

The family of Riemannian spaces, which also includes Euclidean spaces, is itself part of the more general family . These spaces, generally speaking, do not imply the existence of such a quantity as a metric for each of their pairs of points. But their necessary property is the existence of two other structures related to each other - affine connection and curvature. And only under certain conditions on curvature (or connectivity), in such spaces there is a metric. Then these spaces are called Riemannian. In any Riemannian space there is a connection and curvature. But not vice versa.

But one cannot also say that the metric is secondary to connectivity or curvature. No. The existence of a metric is a statement of certain properties of connectivity, and hence of curvature. In the standard interpretation of general relativity, the metric is seen as a more important structure that forms the form of a theory. And the affine connection and curvature turn out to be secondary, derived from the metric. This interpretation was laid down by Einstein, at a time when mathematics had not yet developed a sufficiently advanced and consistent understanding of the hierarchy in terms of the degree of importance of structures that determine the properties of the family of spaces leading to Euclidean ones. Already after the creation of the apparatus of general relativity, primarily by the works of Weyl and Schouten (not theirs alone, of course), the mathematics of spaces with affine connection was developed. Actually, this work was stimulated by the appearance of general relativity. As you can see, the canonical interpretation of the importance of structures in general relativity does not coincide with the current view of mathematics on their relationship. This canonical interpretation is nothing but the identification of certain mathematical structures with physical fields. Giving them a physical meaning.

There are two plans for describing space-time in general relativity. The first of these is space-time itself as the space of events. Events that continuously fill any region of space-time are characterized by four coordinates. Therefore, coordinate systems are assumed to be introduced. The very name of the theory focuses attention precisely on this - the laws of nature that take place in such a space-time must be formulated in the same way with respect to any admissible coordinate system. This requirement is called the principle of general relativity. Note that this plan of the theory does not yet say anything about the presence or absence of a metric in space-time, but already provides the basis for the existence of an affine connection in it (together with curvature and other derivative mathematical structures). Naturally, already at this level, it becomes necessary to give a physical meaning to the mathematical objects of the theory. Here he is. A point in space-time depicts an event, on the one hand, characterized by the position and moment of time, on the other - by four coordinates. Something strange? Isn't it the same thing? But no. In OT it is not the same thing. The most general coordinates allowed in theory cannot be interpreted as positions and moments of time. Such a possibility is postulated only for a very limited group of coordinates - locally inertial, which exist only in the vicinity of each point, but not in the entire area covered by a common coordinate system. This is another postulate of the theory. Here is such a hybrid. I note that it is here that many problems of general relativity are born, but I will not deal with their solution now.

The second plan of the theory can be considered that part of its postulates, which introduces into consideration on space-time a physical phenomenon - gravity, mutual attraction of massive bodies. It is argued that this physical phenomenon can, under certain conditions, be destroyed by a simple choice of an appropriate frame of reference, namely, a locally inertial one. For all bodies having the same acceleration (free fall) due to the presence of a gravitational field of a distant massive body in a small area, this field is not observable in some reference frame. Formally, the postulates end there, but in fact the basic equation of the theory, which introduces the metric into consideration, also refers to the postulates, both as a mathematical statement and as a physical one. Although I'm not going to go into the details of the equation (actually, systems of equations), it's still useful to have it in front of your eyes:

R ik \u003d -с (T ik - 1/2 T g ik)

Here on the left is the so-called Ricci tensor, a certain convolution (combination of constituent components) of the full curvature tensor. With full right it can also be called curvature. On the right is a construction of the energy-momentum tensor (a purely physical quantity in general relativity, singular for massive bodies and external for space-time, which is simply a carrier for energy-momentum in this theory) and a metric that is assumed to exist. Moreover, this metric, as a scalar value produced by the metric tensor, is the same for all points in the region. There is also a dimensional constant c, which is proportional to the gravitational constant. It can be seen from this equation that, by and large, the curvature is compared with the energy-momentum and the metric. The physical meaning of the metric is attributed in GR after the solution of these equations has been obtained. Since in this solution the coefficients of the metric are connected linearly with the potential of the gravitational field (they are calculated through it), then the meaning of the potentials of this field is attributed to the metric tensor. With this approach, curvature should also have a similar meaning. And the affine connection is interpreted as the strength of the field. This interpretation is incorrect, its fallacy is connected with the paradox noted above in the interpretation of coordinates. Naturally, for the theory this does not pass without a trace and manifests itself in a number of well-known problems (non-localization of the energy of the gravitational field, interpretation of singularities), which simply do not arise when geometric quantities are given the correct physical meaning. All this is discussed in more detail in the book ““.

However, in general relativity, the metric willy-nilly, in addition to the meaning artificially imposed on it, has one more physical meaning. Recall what characterizes the metric in the case of a Euclidean space? One very important thing for measurements in space-time is the possibility to introduce in this space a rigid, evenly filling the entire area, rectangular coordinate grid. This grid is called in physics an inertial frame of reference. Such a reference system (coordinate system) corresponds to one and only one standard form of the metric tensor. In frames of reference, arbitrarily moving relative to the inertial one, the form of the metric tensor is different from the standard one. From a physical point of view, the role of the “reference grid” is sufficiently transparent. If you have a rigid body of reference, each point of which is equipped with the same clock, existing in time, then it just implements such a grid. For empty space, we simply invent such a reference body, supplying it (space) with exactly the same metric. In this sense, the metric tensor, which is different from the standard Euclidean one, says that the reference system (coordinates) is built using a non-rigid body, and maybe the clock also runs differently at its points. What do I mean by this? But the fact that the metric tensor is a mathematical image of some of the most important properties of the reference system for us. Those properties that absolutely characterize the structure of the frame of reference itself, allow us to determine how “good” it is, how much it differs from the ideal - the inertial frame. Here GR uses the metric tensor exactly as such an image. How the image of measuring instruments distributed in the frame area, possibly changing its orientation from point to point, but having the same norm everywhere, common to all frame vectors. The metric, considered as a scalar, is this norm, the magnitude of the scale. The metric as a tensor allows us to consider an arbitrary relative movement relative to each other of all scales that make up the reference body. And general relativity describes a situation where it is possible to have such a reference body, real or imaginary, in space-time.

This view of the metric is certainly correct. Moreover, it is also productive, since it immediately draws attention to the agreements remaining in the GTR. Indeed, we have allowed the use of reference systems in which scales at different points can be oriented differently (in a four-dimensional world, orientation also includes movement). And we still require that some absolute characteristic of the scale, its norm (interval) remains the same. Consequently, all the same, the statement of general relativity that it took into consideration all possible frames of reference is excessive. It is not so general, relativity in this theory.

1. The space of isolated points.

Arbitrary set and

2. The set of real numbers with distance forms a metric space.

3. The set of ordered groups of real numbers with is called - dimensional arithmetic Euclidean space.

Proof.

In order to prove that a space is metric, it is necessary to check the satisfiability of the axioms.

Let , , .

, , …, , i.e. .

A3. Let's check if the triangle axiom holds. We write the axiom in the form:

Assuming , , we obtain and .

To prove this inequality, the Cauchy–Bunyakovsky inequality is used.

Really,

Therefore, the triangle axiom is satisfied, and the set under consideration with a given metric is a metric space.

Q.E.D.

4. The set of ordered groups of real numbers with . This metric space is denoted by .

5. The set of ordered groups of real numbers with . This metric space is denoted by .

Examples 3, 4 and 5 show that the same stock of points can be metrized differently.

6. The set of all continuous real functions defined on a segment with distance . This metric space is denoted as the set of points in the space itself: . In particular, instead of writing .

7. Denotes a metric space whose points are all possible sequences of real numbers that satisfy the condition , and the metric is defined by the formula .

Proof.

Since , it makes sense for all . Those. the series converges if and .

Let us show what satisfies the axioms.

Axioms 1, 2 are obvious. The triangle axiom takes the form:

All series are convergent.

The inequality is true for anyone (see example 3). For , we obtain an inequality for .

Q.E.D.

8. Consider the set of all functions that are continuous on the interval and . Such a metric space is denoted and called the space of continuous functions with a quadratic metric.

9. Consider the set of all bounded sequences of real numbers. Let's define . This metric space is denoted by .

10. The set of ordered groups of real numbers with distance , where is any fixed number , is a metric space denoted by .

The metric considered in this example turns into the Euclidean metric for (see Example 3) and into the metric of Example 4 for . It can be shown that the metric (see Example 5) is the limiting case of .

11. Consider all possible sequences of real numbers that satisfy the condition , where is some fixed number, and the distance is determined by the formula . We have a metric space .

12. Let be the set of all infinite sequences of -complex numbers . Let's define . We have a metric space.

Definition: Let be a metric space and be any subset of . Then with the same function , which is now defined for , is a metric space, which is called subspace spaces.

Basic concepts

Denote the metric space by .

Definition: A sequence belonging to a metric space is called fundamental, if each corresponds to a number such that the inequality is true for any .

Definition: A sequence belonging to a metric space is called converging, if there exists such that each corresponds to a number such that the inequality is true for all. Then called limit sequences.

Theorem: If a sequence has a limit, then it is unique.

Proof.

Indeed, if and , then . Since and , then , i.e. .

The theorem has been proven.

Definition: Complete metric space is called the metric space in which every fundamental sequence converges.

Theorem: The metric as a function of two arguments is a continuous function, i.e. if and , then .

Proof:

Let , , , .

By the triangle inequality:

From (1) we get:

From (2) we get:

Because ,

Let's denote .

IN metric space one can consider various sets, neighborhoods of points, limit points, and other concepts of classical analysis.

Definition: Under neighborhood points understand the set containing an open ball of radius centered at the point , i.e.

Definition: The point is called limit point for the set if any neighborhood of the point contains at least one point from , which is different from .

Definition: The point is called internal point sets if it is included in together with some of its neighborhood .

Definition: The set is called open if it consists of only interior points. The set is called closed in itself if it contains all its limit points.

The metric space is closed.

Subspaces may also be non-closed subsets.

If to join all its limit points, then we get the closure .

Definition: A set lying in a metric space is called closed, if it coincides with its closure: .

A closed set is the smallest closed set containing .

Definition: Let . The set is called dense in if . The set is called dense everywhere, If . The set is called nowhere dense in, if whatever the ball is , there is another ball free from the points of the set .

Definition: A space is called separable if it contains an everywhere dense countable set.

In mathematical analysis, an important role is played by the property of the completeness of the real line, that is, the fact that any fundamental sequence of real numbers converges to a certain limit (Cauchy's convergence criterion).

The number line is an example of complete metric spaces.

The spaces of isolated points, , , , , , are complete metric spaces.

Space not complete.

In the analysis, the so-called nested segment lemma :

Let be a system of nested segments. Then for the segment we have .

This means that all segments from the set have a common point.

In the theory of metric spaces, the embedded balls theorem plays a similar role.

Theorem: In order for a metric space to be complete, it is necessary and sufficient that in it any sequence of balls nested into each other, whose radii have a non-empty intersection.

Proof:

Necessity:

Let be a complete metric space and let be a sequence of nested closed balls.

Let be the radius and be the center of the ball.

The sequence of centers is fundamental, since at , and at . Since - is complete, then . Let's say then. Indeed, the ball contains all the points of the sequence , with the possible exception of the points . Thus, the point is the touch point (limit point) for each ball. But since is a closed set, then .

Adequacy:

Let be a fundamental sequence. Let us prove that it has a limit. By virtue of being fundamental, we can choose a point in the sequence such that for all . Let's take the point as the center of a closed ball of radius . Let's denote this ball as . , nested into each other, and the ball - some closed ball of radius contains some point by completion