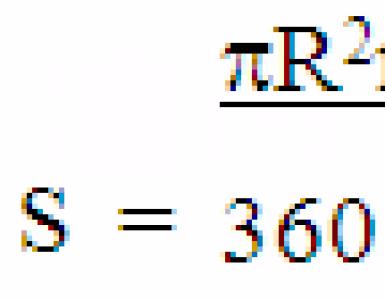Total surface area of ​​the pyramid. Area of ​​a quadrangular pyramid Surface area of ​​a triangular pyramid

Instruction

First of all, it is worth understanding that the side surface of the pyramid is represented by several triangles, the areas of which can be found using a variety of formulas, depending on the known data:

S \u003d (a * h) / 2, where h is the height lowered to side a;

S = a*b*sinβ, where a, b are the sides of the triangle, and β is the angle between these sides;

S \u003d (r * (a + b + c)) / 2, where a, b, c are the sides of the triangle, and r is the radius of the circle inscribed in this triangle;

S \u003d (a * b * c) / 4 * R, where R is the radius of the triangle described around the circle;

S \u003d (a * b) / 2 \u003d r² + 2 * r * R (if the triangle is right-angled);

S = S = (a²*√3)/4 (if the triangle is equilateral).

In fact, these are just the most basic of the known formulas for finding the area of ​​a triangle.

Having calculated, using the above formulas, the areas of all triangles that are the faces of the pyramid, we can begin to calculate the area of ​​\u200b\u200bthis pyramid. This is done extremely simply: you need to add up the areas of all the triangles that form the side surface of the pyramid. This can be expressed in a formula like this:

Sp = ΣSi, where Sp is the lateral area, Si is the area of ​​the i-th triangle, which is part of its lateral surface.

For greater clarity, we can consider a small example: a regular pyramid is given, the side faces of which are formed by equilateral triangles, and at its base lies a square. The length of the edge of this pyramid is 17 cm. It is required to find the area of ​​the lateral surface of this pyramid.

Solution: the length of the edge of this pyramid is known, it is known that its faces are equilateral triangles. Thus, we can say that all sides of all triangles of the lateral surface are 17 cm. Therefore, in order to calculate the area of ​​\u200b\u200bany of these triangles, you will need to apply the formula:

S = (17²*√3)/4 = (289*1.732)/4 = 125.137 cm²

It is known that at the base of the pyramid lies a square. Thus, it is clear that there are four given equilateral triangles. Then the area of ​​the lateral surface of the pyramid is calculated as follows:

125.137 cm² * 4 = 500.548 cm²

Answer: The lateral surface area of ​​the pyramid is 500.548 cm².

First, we calculate the area of ​​the lateral surface of the pyramid. The lateral surface is the sum of the areas of all lateral faces. If you are dealing with a regular pyramid (that is, one that is based on a regular polygon, and the vertex is projected into the center of this polygon), then to calculate the entire side surface, it is enough to multiply the perimeter of the base (that is, the sum of the lengths of all sides of the polygon that lies at the base pyramid) by the height of the side face (otherwise called apothem) and divide the resulting value by 2: Sb = 1/2P*h, where Sb is the area of ​​the side surface, P is the perimeter of the base, h is the height of the side face (apothem).

If you have an arbitrary pyramid in front of you, then you will have to separately calculate the areas of all faces, and then add them up. Since the side faces of the pyramid are triangles, use the formula for the area of ​​a triangle: S=1/2b*h, where b is the base of the triangle and h is the height. When the areas of all the faces are calculated, it remains only to add them up to get the area of ​​​​the side surface of the pyramid.

Then you need to calculate the area of ​​\u200b\u200bthe base of the pyramid. The choice of the formula for the calculation depends on which polygon lies at the base of the pyramid: correct (that is, one whose all sides have the same length) or incorrect. The area of ​​a regular polygon can be calculated by multiplying the perimeter by the radius of the circle inscribed in the polygon and dividing the resulting value by 2: Sn=1/2P*r, where Sn is the area of ​​the polygon, P is the perimeter, and r is the radius of the circle inscribed in the polygon .

A truncated pyramid is a polyhedron formed by a pyramid and its section parallel to the base. Finding the area of ​​the lateral surface of the pyramid is not difficult at all. Its very simple: the area is equal to the product of half the sum of the bases by the apothem. Consider an example of calculating the area of ​​the lateral surface of a truncated pyramid. Suppose we are given a regular quadrangular pyramid. The lengths of the base are b=5 cm, c=3 cm. Apothem a=4 cm. To find the area of ​​the lateral surface of the pyramid, you must first find the perimeter of the bases. In a large base, it will be equal to p1=4b=4*5=20 cm. In a smaller base, the formula will be as follows: p2=4c=4*3=12 cm. Therefore, the area will be equal to: s=1/2(20+12 )*4=32/2*4=64 cm.

A pyramid is a polyhedron, one of whose faces (base) is an arbitrary polygon, and the other faces (sides) are triangles with a common vertex. According to the number of corners of the base of the pyramid, there are triangular (tetrahedron), quadrangular, and so on.

The pyramid is a polyhedron with a base in the form of a polygon, and the remaining faces are triangles with a common vertex. The apothem is the height of the side face of a regular pyramid, which is drawn from its top.

The area of ​​the lateral surface of a regular pyramid is equal to the product of its apothem by half the perimeter of the base.

As for the total surface area, we simply add the base area to the side.

The lateral surface of a regular pyramid is equal to the product of the semiperimeter of the base and the apothem.

Proof:

If the side of the base is a, the number of sides is n, then the side surface of the pyramid is:

a l n/2 =a n l/2=pl/2

where l is the apothem and p is the perimeter of the base of the pyramid. The theorem has been proven.

This formula reads like this:

The area of ​​the lateral surface of a regular pyramid is equal to half the product of the perimeter of the base and the apothem of the pyramid.

The total surface area of ​​the pyramid is calculated by the formula:

S full =S side +S main

If the pyramid is irregular, then its lateral surface will be equal to the sum of the areas of its lateral faces.

Pyramid Volume

Volume pyramid is equal to one third of the product of the area of ​​​​the base and the height.

Proof. We will start from a triangular prism. Draw a plane through the vertex A "of the upper base of the prism and the opposite edge BC of the lower base. This plane will cut off the triangular pyramid A" ABC from the prism. We decompose the remaining part of the prism into the core of the body by drawing a plane through the diagonals A "C" and "B" C of the side faces. The resulting two bodies are also pyramids. Considering the triangle A"B"C" as the base of one of them, and C its top, we will see that its base and height are the same as those of the first pyramid we cut off, therefore pyramids A"ABC and CA"B"C" are equal. In addition, both new pyramids CA "B" C "and A" B "BC" are also equal in size - this will become clear if we take the triangles BC "and B" CC "for their bases. Pyramids CA" B "C" and A "B "VS have a common vertex A", and their bases are located in the same plane and are equal, therefore, the pyramids are equal in size. So, the prism is decomposed into three pyramids of equal size to each other, the volume of each of them is equal to one third of the volume of the prism. Since the shape of the base is insignificant, then, in general, the volume of an n-gonal pyramid is equal to one third of the volume of a prism with the same height and the same (or equal) base.Recalling the formula expressing the volume of a prism, V=Sh, we get the final result: V=1/3Sh

Before studying questions about this geometric figure and its properties, it is necessary to understand some terms. When a person hears about the pyramid, he imagines huge buildings in Egypt. This is what the simplest ones look like. But they come in different types and shapes, which means that the calculation formula for geometric shapes will be different.

Figure types

Pyramid - geometric figure, denoting and representing multiple faces. In fact, this is the same polyhedron, at the base of which lies a polygon, and on the sides there are triangles that connect at one point - the vertex. The figure is of two main types:

• correct;
• truncated.

In the first case, the base is a regular polygon. Here all side surfaces are equal between themselves and the figure itself will please the eye of a perfectionist.

In the second case, there are two bases - a large one at the very bottom and a small one between the top, repeating the shape of the main one. In other words, a truncated pyramid is a polyhedron with a section formed parallel to the base.

Terms and notation

Basic terms:

• Regular (equilateral) triangle A figure with three identical angles and equal sides. In this case, all angles are 60 degrees. The figure is the simplest of the regular polyhedra. If this figure lies at the base, then such a polyhedron will be called a regular triangular one. If the base is a square, the pyramid will be called a regular quadrangular pyramid.
• Vertex- the highest point where the edges meet. The height of the top is formed by a straight line emanating from the top to the base of the pyramid.
• edge is one of the planes of the polygon. It can be in the form of a triangle in the case of a triangular pyramid, or in the form of a trapezoid for a truncated pyramid.
• cross section- a flat figure formed as a result of dissection. Not to be confused with a section, as a section also shows what is behind the section.
• Apothem- a segment drawn from the top of the pyramid to its base. It is also the height of the face where the second height point is. This definition is valid only in relation to a regular polyhedron. For example - if it is not a truncated pyramid, then the face will be a triangle. In this case, the height of this triangle will become an apothem.

Area formulas

Find the area of ​​the lateral surface of the pyramid any type can be done in several ways. If the figure is not symmetrical and is a polygon with different sides, then in this case it is easier to calculate the total surface area through the totality of all surfaces. In other words, you need to calculate the area of ​​\u200b\u200beach face and add them together.

Depending on what parameters are known, formulas for calculating a square, a trapezoid, an arbitrary quadrilateral, etc. may be required. The formulas themselves in different cases will also be different.

In the case of a regular figure, finding the area is much easier. It is enough to know just a few key parameters. In most cases, calculations are required precisely for such figures. Therefore, the corresponding formulas will be given below. Otherwise, you would have to paint everything on several pages, which will only confuse and confuse.

Basic formula for calculation the lateral surface area of ​​a regular pyramid will look like this:

S \u003d ½ Pa (P is the perimeter of the base, and is the apothem)

Let's consider one of the examples. The polyhedron has a base with segments A1, A2, A3, A4, A5, and they are all equal to 10 cm. Let the apothem be equal to 5 cm. First you need to find the perimeter. Since all five faces of the base are the same, it can be found as follows: P \u003d 5 * 10 \u003d 50 cm. Next, we apply the basic formula: S \u003d ½ * 50 * 5 \u003d 125 cm squared.

Lateral surface area of ​​a regular triangular pyramid the easiest to calculate. The formula looks like this:

S =½* ab *3, where a is the apothem, b is the facet of the base. The factor of three here means the number of faces of the base, and the first part is the area of ​​the side surface. Consider an example. Given a figure with an apothem of 5 cm and a base face of 8 cm. We calculate: S = 1/2 * 5 * 8 * 3 = 60 cm squared.

Lateral surface area of ​​a truncated pyramid it's a little more difficult to calculate. The formula looks like this: S \u003d 1/2 * (p _01 + p _02) * a, where p_01 and p_02 are the perimeters of the bases, and is the apothem. Consider an example. Suppose, for a quadrangular figure, the dimensions of the sides of the bases are 3 and 6 cm, the apothem is 4 cm.

Here, for starters, you should find the perimeters of the bases: p_01 \u003d 3 * 4 \u003d 12 cm; p_02=6*4=24 cm. It remains to substitute the values ​​into the main formula and get: S =1/2*(12+24)*4=0.5*36*4=72 cm squared.

Thus, it is possible to find the lateral surface area of ​​a regular pyramid of any complexity. Be careful not to confuse these calculations with the total area of ​​the entire polyhedron. And if you still need to do this, it’s enough to calculate the area of ​​\u200b\u200bthe largest base of the polyhedron and add it to the area of ​​\u200b\u200bthe lateral surface of the polyhedron.

Video

To consolidate information on how to find the lateral surface area of ​​different pyramids, this video will help you.

In this lesson:

• Task 1. Find the total surface area of ​​the pyramid
• Task 2. Find the area of ​​the lateral surface of a regular triangular pyramid

See also related materials:
.

Note . If you need to solve a problem in geometry, which is not here - write about it in the forum. In tasks, instead of the "square root" symbol, the sqrt () function is used, in which sqrt is the square root symbol, and the radical expression is indicated in brackets. For simple radical expressions, the sign "√" can be used.

Task 1. Find the total surface area of ​​a regular pyramid

The height of the base of a regular triangular pyramid is 3 cm, and the angle between the side face and the base of the pyramid is 45 degrees.
Find the total surface area of ​​the pyramid

Solution.

At the base of a regular triangular pyramid lies an equilateral triangle.
Therefore, to solve the problem, we use the properties of a regular triangle:

We know the height of the triangle, from where we can find its area.
h = √3/2a
a = h / (√3/2)
a = 3 / (√3/2)
a = 6 / √3

From where the area of ​​​​the base will be equal to:
S = √3/4 a 2
S = √3/4 (6 / √3) 2
S = 3√3

In order to find the area of ​​the side face, we calculate the height KM. The OKM angle, according to the problem statement, is 45 degrees.
Thus:
OK / MK = cos 45
Let's use the table of values ​​of trigonometric functions and substitute the known values.

OK / MK = √2/2

We take into account that OK is equal to the radius of the inscribed circle. Then
OK = √3/6 a
OK = √3/6 * 6/√3 = 1

Then
OK / MK = √2/2
1 / MK = √2/2
MK = 2/√2

The area of ​​the side face is then equal to half the product of the height and the base of the triangle.
Sside = 1/2 (6 / √3) (2/√2) = 6/√6

Thus, the total surface area of ​​the pyramid will be equal to
S = 3√3 + 3 * 6/√6
S = 3√3 + 18/√6

Answer: 3√3 + 18/√6

Task 2. Find the lateral surface area of ​​a regular pyramid

In a regular triangular pyramid, the height is 10 cm, and the side of the base is 16 cm . Find the lateral surface area .

Solution.

Since the base of a regular triangular pyramid is an equilateral triangle, then AO is the radius of the circumscribed circle around the base.
(It follows from)

The radius of a circle circumscribed around an equilateral triangle is found from its properties

Whence the length of the edges of a regular triangular pyramid will be equal to:
AM 2 = MO 2 + AO 2
the height of the pyramid is known by the condition (10 cm), AO = 16√3/3
AM 2 = 100 + 256/3
AM = √(556/3)

Each side of the pyramid is an isosceles triangle. The area of ​​an isosceles triangle is found from the first formula below

S = 1/2 * 16 sqrt((√(556/3) + 8) (√(556/3) - 8))
S = 8 sqrt((556/3) - 64)
S = 8 sqrt(364/3)
S = 16 sqrt(91/3)

Since all three faces of a regular pyramid are equal, the lateral surface area will be equal to
3S = 48√(91/3)

Answer: 48 √(91/3)

Task 3. Find the total surface area of ​​a regular pyramid

The side of a regular triangular pyramid is 3 cm and the angle between the side face and the base of the pyramid is 45 degrees. Find the total surface area of ​​the pyramid.

Solution.
Since the pyramid is regular, it has an equilateral triangle at its base. So the area of ​​the base is


So = 9 * √3/4

In order to find the area of ​​the side face, we calculate the height KM. The OKM angle, according to the problem statement, is 45 degrees.
Thus:
OK / MK = cos 45
Let's use

The video course "Get an A" includes all the topics necessary for the successful passing of the exam in mathematics by 60-65 points. Completely all tasks 1-13 of the Profile USE in mathematics. Also suitable for passing the Basic USE in mathematics. If you want to pass the exam with 90-100 points, you need to solve part 1 in 30 minutes and without mistakes!

Preparation course for the exam for grades 10-11, as well as for teachers. Everything you need to solve part 1 of the exam in mathematics (the first 12 problems) and problem 13 (trigonometry). And this is more than 70 points on the Unified State Examination, and neither a hundred-point student nor a humanist can do without them.

All the necessary theory. Quick solutions, traps and secrets of the exam. All relevant tasks of part 1 from the Bank of FIPI tasks have been analyzed. The course fully complies with the requirements of the USE-2018.

The course contains 5 large topics, 2.5 hours each. Each topic is given from scratch, simply and clearly.

Hundreds of exam tasks. Text problems and probability theory. Simple and easy to remember problem solving algorithms. Geometry. Theory, reference material, analysis of all types of USE tasks. Stereometry. Cunning tricks for solving, useful cheat sheets, development of spatial imagination. Trigonometry from scratch - to task 13. Understanding instead of cramming. Visual explanation of complex concepts. Algebra. Roots, powers and logarithms, function and derivative. Base for solving complex problems of the 2nd part of the exam.