Что делать если у логарифмов разные основания. Разбираемся с натуральным логарифмом. Основные свойства логарифмов

Определение логарифма

Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить b .

Числом е в математике принято обозначать предел, к которому стремиться выражение

Число е является иррациональным числом - числом, несоизмеримым с единицей, оно не может быть точно выраженным ни целым ни дробным рациональным числом.

Буква е - первая буква латинского слова exponere - выставлять напоказ, отсюда в математике название экспоненциальная - показательная функция.

Число е широко применяется в математике, и во всех науках, так или иначе применяющих для своих нужд математические расчеты.

Логарифмы. Свойства логарифмов

Определение: Логарифмом положительного числа b по основанию называется показатель степени с, в которую надо возвести число а, чтобы получить число b.

Основное логарифмическое тождество:

7) Формула перехода к новому основанию:

lna = log e a, e ≈ 2,718…

Задачи и тесты по теме «Логарифмы. Свойства логарифмов»

• Логарифмы — Важные темы для повторения ЕГЭ по математике

Для успешного выполнения заданий по данной теме Вы должны знать определение логарифма, свойства логарифмов, основное логарифмическое тождество, определения десятичного и натурального логарифмов. Основные типы задач по данной теме — это задачи на вычисление и преобразование логарифмических выражений. Рассмотрим их решение на следующих примерах.

Решение: Используя свойства логарифмов, получим

Решение: используя свойства степени, получим

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Свойства логарифмов, формулировки и доказательства.

Логарифмы обладают рядом характерных свойств. В этой статье мы разберем основные свойства логарифмов . Здесь мы дадим их формулировки, запишем свойства логарифмов в виде формул, покажем примеры их применения, а также приведем доказательства свойств логарифмов.

Навигация по странице.

Основные свойства логарифмов, формулы

Для удобства запоминания и использования представим основные свойства логарифмов в виде списка формул. В следующем пункте дадим их формулировки, доказательства, примеры использования и необходимые пояснения.

Свойство логарифма единицы: log a 1=0 для любого a>0 , a≠1 .

Логарифм числа, равного основанию: log a a=1 при a>0 , a≠1 .

Свойство логарифма степени основания: log a a p =p , где a>0 , a≠1 и p – любое действительное число.

Логарифм произведения двух положительных чисел: log a (x·y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
и свойство логарифма произведения n положительных чисел: log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Свойство логарифма частного: , где a>0 , a≠1 , x>0 , y>0 .

Логарифм степени числа: log a b p =p·log a |b| , где a>0 , a≠1 , b и p такие числа, что степень b p имеет смысл и b p >0 .

Следствие: , где a>0 , a≠1 , n – натуральное число, большее единицы, b>0 .

Следствие 1: , a>0 , a≠1 , b>0 , b≠1 .

Следствие 2: , a>0 , a≠1 , b>0 , p и q – действительные числа, q≠0 , в частности при b=a имеем .

Формулировки и доказательства свойств

Переходим к формулированию и доказательству записанных свойств логарифмов. Все свойства логарифмов доказываются на основе определения логарифма и вытекающего из него основного логарифмического тождества, а также свойств степени.

Начнем со свойства логарифма единицы . Его формулировка такова: логарифм единицы равен нулю, то есть, log a 1=0 для любого a>0 , a≠1 . Доказательство не вызывает сложностей: так как a 0 =1 для любого a , удовлетворяющего указанным выше условиям a>0 и a≠1 , то доказываемое равенство log a 1=0 сразу следует из определения логарифма.

Приведем примеры применения рассмотренного свойства: log 3 1=0 , lg1=0 и .

Переходим к следующему свойству: логарифм числа, равного основанию, равен единице , то есть, log a a=1 при a>0 , a≠1 . Действительно, так как a 1 =a для любого a , то по определению логарифма log a a=1 .

Примерами использования этого свойства логарифмов являются равенства log 5 5=1 , log 5,6 5,6 и lne=1 .

Логарифм степени числа, равного основанию логарифма, равен показателю степени . Этому свойству логарифма отвечает формула вида log a a p =p , где a>0 , a≠1 и p – любое действительное число. Это свойство напрямую следует из определения логарифма. Заметим, что оно позволяет сразу указать значение логарифма, если есть возможность представить число под знаком логарифма в виде степени основания, подробнее об этом мы поговорим в статье вычисление логарифмов.

К примеру, log 2 2 7 =7 , lg10 -4 =-4 и .

Логарифм произведения двух положительных чисел x и y равен произведению логарифмов этих чисел: log a (x·y)=log a x+log a y , a>0 , a≠1 . Докажем свойство логарифма произведения. В силу свойств степени a log a x+log a y =a log a x ·a log a y , а так как по основному логарифмическому тождеству a log a x =x и a log a y =y , то a log a x ·a log a y =x·y . Таким образом, a log a x+log a y =x·y , откуда по определению логарифма вытекает доказываемое равенство.

Покажем примеры использования свойства логарифма произведения: log 5 (2·3)=log 5 2+log 5 3 и .

Свойство логарифма произведения можно обобщить на произведение конечного числа n положительных чисел x 1 , x 2 , …, x n как log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n . Данное равенство без проблем доказывается методом математической индукции.

Например, натуральных логарифм произведения можно заменить суммой трех натуральных логарифмов чисел 4 , e , и .

Логарифм частного двух положительных чисел x и y равен разности логарифмов этих чисел. Свойству логарифма частного соответствует формула вида , где a>0 , a≠1 , x и y – некоторые положительные числа. Справедливость этой формулы доказывается как и формула логарифма произведения: так как , то по определению логарифма .

Приведем пример использования этого свойства логарифма: .

Переходим к свойству логарифма степени . Логарифм степени равен произведению показателя степени на логарифм модуля основания этой степени. Запишем это свойство логарифма степени в виде формулы: log a b p =p·log a |b| , где a>0 , a≠1 , b и p такие числа, что степень b p имеет смысл и b p >0 .

Сначала докажем это свойство для положительных b . Основное логарифмическое тождество позволяет нам представить число b как a log a b , тогда b p =(a log a b) p , а полученное выражение в силу свойство степени равно a p·log a b . Так мы приходим к равенству b p =a p·log a b , из которого по определению логарифма заключаем, что log a b p =p·log a b .

Осталось доказать это свойство для отрицательных b . Здесь замечаем, что выражение log a b p при отрицательных b имеет смысл лишь при четных показателях степени p (так как значение степени b p должно быть больше нуля, в противном случае логарифм не будет иметь смысла), а в этом случае b p =|b| p . Тогда b p =|b| p =(a log a |b|) p =a p·log a |b| , откуда log a b p =p·log a |b| .

Например, и ln(-3) 4 =4·ln|-3|=4·ln3 .

Из предыдущего свойства вытекает свойство логарифма из корня : логарифм корня n -ой степени равен произведению дроби 1/n на логарифм подкоренного выражения, то есть, , где a>0 , a≠1 , n – натуральное число, большее единицы, b>0 .

Доказательство базируется на равенстве (смотрите определение степени с дробным показателем), которое справедливо для любых положительных b , и свойстве логарифма степени: .

Вот пример использования этого свойства: .

Теперь докажем формулу перехода к новому основанию логарифма вида . Для этого достаточно доказать справедливость равенства log c b=log a b·log c a . Основное логарифмическое тождество позволяет нам число b представить как a log a b , тогда log c b=log c a log a b . Осталось воспользоваться свойством логарифма степени: log c a log a b =log a b·log c a . Так доказано равенство log c b=log a b·log c a , а значит, доказана и формула перехода к новому основанию логарифма .

Покажем пару примеров применения этого свойства логарифмов: и .

Формула перехода к новому основанию позволяет переходить к работе с логарифмами, имеющими «удобное» основание. Например, с ее помощью можно перейти к натуральным или десятичным логарифмам, чтобы можно было вычислить значение логарифма по таблице логарифмов. Формула перехода к новому основанию логарифма также позволяет в некоторых случаях находить значение данного логарифма, когда известны значения некоторых логарифмов с другими основаниями.

Часто используется частный случай формулы перехода к новому основанию логарифма при c=b вида . Отсюда видно, что log a b и log b a – взаимно обратные числа. К примеру, .

Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a: .

Осталось доказать свойства сравнения логарифмов.

Воспользуемся методом от противного. Предположим, что при a 1 >1 , a 2 >1 и a 1 2 и при 0 1 справедливо log a 1 b≤log a 2 b . По свойствам логарифмов эти неравенства можно переписать как и соответственно, а из них следует, что log b a 1 ≤log b a 2 и log b a 1 ≥log b a 2 соответственно. Тогда по свойствам степеней с одинаковыми основаниями должны выполняться равенства b log b a 1 ≥b log b a 2 и b log b a 1 ≥b log b a 2 , то есть, a 1 ≥a 2 . Так мы пришли к противоречию условию a 1 2 . На этом доказательство завершено.

Основные свойства логарифмов

• Материалы к уроку
• Скачать все формулы

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы - это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами .

Эти правила обязательно надо знать - без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного - все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log a x и log a y . Тогда их можно складывать и вычитать, причем:

Итак, сумма логарифмов равна логарифму произведения, а разность - логарифму частного. Обратите внимание: ключевой момент здесь - одинаковые основания . Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры - и убедитесь:

Задача. Найдите значение выражения: log 6 4 + log 6 9.

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log 6 4 + log 6 9 = log 6 (4 · 9) = log 6 36 = 2.

Задача. Найдите значение выражения: log 2 48 − log 2 3.

Основания одинаковые, используем формулу разности:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Задача. Найдите значение выражения: log 3 135 − log 3 5.

Снова основания одинаковые, поэтому имеем:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные - подобные выражения на полном серьезе (иногда - практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

• log a x n = n · log a x ;
• 
• 

Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить - в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Задача. Найдите значение выражения: log 7 49 6 .

Избавимся от степени в аргументе по первой формуле:
log 7 49 6 = 6 · log 7 49 = 6 · 2 = 12

Задача. Найдите значение выражения:

[Подпись к рисунку]

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 2 4 ; 49 = 7 2 . Имеем:

[Подпись к рисунку]

Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели - получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log 2 7. Поскольку log 2 7 ≠ 0, можем сократить дробь - в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

Пусть дан логарифм log a x . Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:

[Подпись к рисунку]

В частности, если положить c = x , получим:

[Подпись к рисунку]

Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача. Найдите значение выражения: log 5 16 · log 2 25.

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

А теперь «перевернем» второй логарифм:

[Подпись к рисунку]

Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Задача. Найдите значение выражения: log 9 100 · lg 3.

Основание и аргумент первого логарифма - точные степени. Запишем это и избавимся от показателей:

[Подпись к рисунку]

Теперь избавимся от десятичного логарифма, перейдя к новому основанию:

[Подпись к рисунку]

Основное логарифмическое тождество

Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

1. n = log a a n

2. В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.

   Вторая формула - это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество.

   В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a ? Правильно: получится это самое число a . Внимательно прочитайте этот абзац еще раз - многие на нем «зависают».

   Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.

   [Подпись к рисунку]

   Заметим, что log 25 64 = log 5 8 - просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:

   [Подпись к рисунку]

   Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂

   Логарифмическая единица и логарифмический ноль

   В заключение приведу два тождества, которые сложно назвать свойствами - скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

   1. log a a = 1 - это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
   2. log a 1 = 0 - это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица - логарифм равен нулю! Потому что a 0 = 1 - это прямое следствие из определения.

   Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее - и решайте задачи.

   Логарифм. Свойства логарифма (сложение и вычитание).

   Свойства логарифма вытекают из его определения. И так логарифм числа b по основанию а определяется как показатель степени, в которую надо возвести число a , чтобы получить число b (логарифм существует только у положительных чисел).

   Из данной формулировки следует, что вычисление x=log a b , равнозначно решению уравнения a x =b. Например, log 2 8 = 3 потому, что 8 = 2 3 . Формулировка логарифма дает возможность обосновать, что если b=a с , то логарифм числа b по основанию a равен с . Также ясно, что тема логарифмирования тесно взаимосвязана с темой степени числа.

   С логарифмами, как и с любыми числами, можно выполнять операции сложения, вычитания и всячески трансформировать. Но ввиду того, что логарифмы — это не совсем ординарные числа, здесь применимы свои особенные правила, которые называются основными свойствами .

   Сложение и вычитание логарифмов.

   Возьмем два логарифма с одинаковыми основаниями: log a x и log a y . Тогда сними возможно выполнять операции сложения и вычитания:

   Как видим, сумма логарифмов равняется логарифму произведения, а разность логарифмов — логарифму частного. Причем это верно если числа а , х и у положительны и а ≠ 1.

   Важно обращать внимание, что основным аспектом в данных формулах выступают одни и те же основания. Если основания отличаются друг от друга, эти правила не применимы!

   Правила сложения и вычитания логарифмов с одинаковыми основаниями читаются не только с лева на право, но и на оборот. В результате мы имеем теоремы логарифма произведения и логарифма частного.

   Логарифм произведения двух положительных чисел равен сумме их логарифмов; перефразируя данную теорему получим следующее, если числа а , x и у положительны и а ≠ 1 , то:

   Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. Говоря по другому, если числа а , х и у положительны и а ≠ 1 , то:

   Применим вышеизложенные теоремы для решения примеров :

   Если числа x и у отрицательны, то формула логарифма произведения становится бессмысленной. Так, запрещено писать:

   так как выражения log 2 (-8) и log 2 (-4) вообще не определены (логарифмическая функция у = log 2 х определена лишь для положительных значений аргументах ).

   Теорема произведения применима не только для двух, но и для неограниченного числа сомножителей. Это означает, что для всякого натурального k и любых положительных чисел x 1 , x 2 , . . . ,x n существует тождество:

   Из теоремы логарифма частного можно получить еще одно свойство логарифма. Общеизвестно, что log a 1= 0, следовательно,

   А значит имеет место равенство:

   Логарифмы двух взаимно обратных чисел по одному и тому же основанию будут различны друг от друга исключительно знаком. Так:

   Логарифм. Свойства логарифмов

   Логарифм. Свойства логарифмов

   Рассмотрим равенство . Пусть нам известны значения и и мы хотим найти значение .

   То есть мы ищем показатель степени, в которую нужно взвести чтобы получить .

   Пусть переменная может принимать любое действительное значение, тогда на переменные и накладываются такие ограничения: o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   Если нам известны значения и , и перед нами стоит задача найти неизвестное , то для этой цели вводится математическое действие, которое называется логарифмирование .

   Чтобы найти значение , мы берем логарифм числа по основанию :

   Логарифмом числа по основанию называется показатель степени, в которую надо возвести , чтобы получить .

   То есть основное логарифмическое тождество :

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   является по сути математической записью определения логарифма .

   Математическая операция логарифмирование является обратной по отношению к операции возведения в степень, поэтому свойства логарифмов тесно связаны со свойствами степени.

   Перечислим основные свойства логарифмов :

   (o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ title=»d1″/>

   4.

   5.

   Следующая группа свойств позволяет представить показатель степени выражения, стоящего под знаком логарифма, или стоящего в основании логарифма в виде коэффициента перед знаком логарифма:

   6.

   7.

   8.

   9.

   Следующая группа формул позволяет перейти от логарифма с данным основанием к логарифму с произвольным основанием, и называется формулами перехода к новому основанию :

   10.

   12. (следствие из свойства 11)

   

   Следующие три свойства не очень известны, однако они часто используются при решении логарифмических уравнений, или при упрощении выражений, содержащих логарифмы:

   13.

   14.

   15.

   Частные случаи:

   — десятичный логарифм

   — натуральный логарифм

   При упрощении выражений, содержащих логарифмы применяется общий подход:

   1. Представляем десятичные дроби в виде обыкновенных.

   2. Смешанные числа представляем в виде неправильных дробей.

   3. Числа, стоящие в основании логарифма и под знаком логарифма раскладываем на простые множители.

   4. Стараемся привести все логарифмы к одному основанию.

   5. Применяем свойства логарифмов.

   Давайте рассмотрим примеры упрощения выражений, содержащих логарифмы.

   Пример 1.

   Вычислить:

   Упростим все показатели степеней: наша задача привести их к логарифмам, в основании которых стоит то же число, что и в основании степtни.

   ==(по свойству 7)=(по свойству 6) =

   Подставим показатели, которые у нас получились в исходное выражение. Получим:

   Ответ: 5,25

   Пример 2. Вычислить:

   

   Приведем все логарифмы к основанию 6 (при этом логарифмы из знаменателя дроби «перекочуют» в числитель):

   Разложим числа, стоящие под знаком логарифма на простые множители:

   Применим свойства 4 и 6:

   Введем замену

   Получим:

   Ответ: 1

   Логарифм . Основное логарифмическое тождество.

   Свойства логарифмов. Десятичный логарифм. Натуральный логарифм.

   Логарифмом положительного числа N по основанию (b > 0, b 1) называется показатель степени x , в которую нужно возвести b , чтобы получить N .

   Эта запись равнозначна следующей: b x = N .

   П р и м е р ы: log 3 81 = 4 , так как 3 4 = 81 ;

   log 1/3 27 = – 3 , так как (1/3) — 3 = 3 3 = 27 .

   Вышеприведенное определение логарифма можно записать в виде тождества:

   

   Основные свойства логарифмов.

   2) log 1 = 0 , так как b 0 = 1 .

   3) Логарифм произведения равен сумме логарифмов сомножителей:

   4) Логарифм частного равен разности логарифмов делимого и делителя:

   5) Логарифм степени равен произведению показателя степени на логарифм её основания:

   Следствием этого свойства является следующее: логарифм корня равен логарифму подкоренного числа, делённому на степень корня:

   

   6) Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак лога рифма:

   

   Два последних свойства можно объединить в одно:

   

   7) Формула модуля перехода (т. e . перехода от одного основания логарифма к другому основанию):

   

   В частном случае при N = a имеем:

   

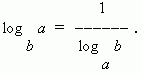
   Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg , т.е. log 10 N = lg N . Логарифмы чисел 10, 100, 1000, . p авны соответственно 1, 2, 3, …, т.е. имеют столько положительных

   единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1, 0.01, 0.001, . p авны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц, сколько нулей стоит в логарифмируемом числе перед единицей (считая и нуль целых). Логарифмы остальных чисел имеют дробную часть, называемую мантиссой . Целая часть логарифма называется характеристикой . Для практического при менения десятичные логарифмы наиболее удобны.

   Натуральным логарифмом называется логарифм по основанию е . Он обозначается ln , т.е. log e N = ln N . Число е является иррациональным, его приближённое значение 2.718281828. Оно является пределом, к которому стремится число (1 + 1 / n ) n при неограниченном возрастании n (см. первый замечательный предел на странице «Пределы числовых последовательностей»).
   Как это ни покажется странным, натуральные логарифмы оказались очень удобными при проведении различного рода операций, связанных с анализом функций. Вычисление логарифмов по основанию е осуществляется гораздо быстрее, чем по любому другому основанию.

• Как получить свидетельство о государственной регистрации права собственности на квартиру? В соответствии с Конституцией РФ на государство возложена функция гаранта права частной собственности. Свои полномочия в этой сфере государство […] Штраф за несдачу отчетности СЗВ-М и РСВ-1 в ПФР По завершению каждого отчетного и расчетного периодов страхователь в обязательном порядке должен предоставить в Пенсионный фонд необходимый расчет по форме РСВ-1. Если по каким-либо причинам […]
• Когда и как получить накопительную часть пенсии в Сбербанке? Сбербанк является банком-партнером государственного пенсионного фонда. На основании этого граждане, оформившие накопительную пенсию, могли переводить в него накопительную часть […]
• Как получить субсидии на оплату коммунальных услуг (квартплату)? Субсидии на оплату коммунальных услуг предоставляются определенным категориям граждан в соответствии с жилищным законодательством РФ. Чтобы узнать подробности о процедуре […]
• Сведения бесплатно по ИНН или ОГРН из реестра налоговой по всей России - онлайн На Едином портале Налоговых услуг могут быть получены сведения о государственной регистрации юридических лиц, индивидуальных предпринимателей, […]
• Выгребная яма: санитарные и строительные нормы и правила Для обустройства канализации на дачном или городском участке нужно следовать не только строительным, но и законодательным стандартам. Выгребная яма: нормы и правила её обустройства […]

Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения .

Сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства:

Теперь на основе этих формул(свойств), покажем примеры решения логарифмов .

Примеры решения логарифмов на основании формул.

Логарифм положительного числа b по основанию a (обозначается log a b) - это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.

Согласно определения log a b = x, что равносильно a x = b, поэтому log a a x = x.

Логарифмы , примеры:

log 2 8 = 3, т.к. 2 3 = 8

log 7 49 = 2, т.к. 7 2 = 49

log 5 1/5 = -1, т.к. 5 -1 = 1/5

Десятичный логарифм - это обычный логарифм, в основании которого находится 10. Обозначается как lg.

log 10 100 = 2, т.к. 10 2 = 100

Натуральный логарифм - также обычный логарифм логарифм, но уже с основанием е (е = 2,71828... - иррациональное число). Обозначается как ln.

Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.

• Основное логарифмическое тождество
  a log a b = b

  8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9

• Логарифм произведения равен сумме логарифмов
  log a (bc) = log a b + log a c

  log 3 8,1 + log 3 10 = log 3 (8,1*10) = log 3 81 = 4

• Логарифм частного равен разности логарифмов
  log a (b/c) = log a b - log a c

  9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81

• Свойства степени логарифмируемого числа и основания логарифма

  Показатель степени логарифмируемого числа log a b m = mlog a b

  Показатель степени основания логарифма log a n b =1/n*log a b

  log a n b m = m/n*log a b,

  если m = n, получим log a n b n = log a b

  log 4 9 = log 2 2 3 2 = log 2 3

• Переход к новому основанию
  log a b = log c b/log c a,

  если c = b, получим log b b = 1

  тогда log a b = 1/log b a

  log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1

Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: " ". Не пропустите!

Если у вас остались вопросы по решению, пишите их в комментариях к статье.

Заметка: решили получить образование другого класса обучение за рубежом как вариант развития событий.

Задача 1. Найти положительный корень уравнения x 4 = 81
По определению арифметического корня имеем \(x = \sqrt{81} = 3 \)

Задача 2. Решить уравнение 3 x = 81
Запишем данное уравнение так: 3 x = 3 4 , откуда x = 4

В задаче 1 неизвестным является основание степени, а в задаче 2 - показатель степени. Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3. Но уже, например, уравнение 3 x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.
Уравнение a x = b, где a > 0, \(a \neq 1 \), b > 0, имеет единственный корень. Этот корень называют логарифмом числа b no основанию a и обозначают log a b
Например, корнем уравнения 3 x = 81 является число 4, т.е. log 3 81 = 4.

Определение. Логарифмом положительного числа b по основанию a, где a > 0, \(a \neq 1 \), называется показатель степени, в которую надо возвести число a, чтобы получить b

Например:

log 2 8 = 3, так как 2 3 = 8
\(\log_3 \frac{1}{9} = -2 \), так как \(3^{-2} = \frac{1}{9} \)
log 7 7 = 1, так как 7 1 = 7

Определение логарифма можно записать так:
$$ a^{\log_a b} = b $$ Это равенство справедливо при b > 0, b > 0, \(a \neq 1 \). Его обычно называют основным логарифмическим тождеством.

Действие нахождения логарифма числа называют логарифмированием.
Действие нахождения числа по его логарифму называют потенцированием.

Вычислить log 64 128
Обозначим log 64 128 = х. По определению логарифма 64 x = 128. Так как 64 = 2 6 , 128 = 2 7 , то 2 6x = 2 7 , откуда 6x = 7, х = 7/6.
Ответ log 64 128 = 7/6

Вычислить \(3^{-2\log_3 5} \)
Используя свойства степени и основное логарифмическое тождество, находим

$$ 3^{-2\log_3 5} = \left(3^{\log_3 5} \right)^{-2} = 5^{-2} = \frac{1}{25}$$

Решить уравнение log 3 (1-x) = 2
По определению логарифма 3 2 = 1 - x, откуда x = -8

Свойства логарифмов

При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.

Пусть а > 0, \(a \neq 1 \), b > 0, c > 0, r - любое действительное число. Тогда справедливы формулы:

1) log a (bc) = log a b + log a c

2) \(\log_a \frac{b}{c} = \log_a b - \log_a c \)
3) log a b r = r log a b

Десятичные и натуральные логарифмы

Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора. И в том и в другом случае находятся только десятичные или натуральные логарифмы.

Определение. Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут
lg b вместо log 10 b

Определение. Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e - иррациональное число, приближённо равное 2,7. При этом пишут ln b вместо log e b

Иррациональное число e играет важную роль в математике и её приложениях. Число e можно представить как сумму:
$$ e = 1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} + \dots + \frac{1}{1 \cdot 2 \cdot 3 \cdot \dots \cdot n} + \dots $$

или $$ e = \sum_{n=0}^{\infty} \frac{1}{n!} $$ $$ e \approx 2,7182818284 $$

Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы чисел по любому основанию.
Для этого используется формула замены основания логарифма:

$$ \log_a b = \frac{\log_c b}{\log_c a} $$ где b > 0, a > 0, \(a \neq 1 \), c > 0, \(c \neq 1 \)

Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ \log_a b = \frac{\lg b}{\lg a} , \;\; \log_a b = \frac{\ln b}{\ln a} $$

Логарифмическая функция, её свойства и график

В математике и её приложениях часто встречается логарифмическая функция
y = log a x
где а - заданное число, a > 0, \(a \neq 1 \)

Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции - множество всех положительных чисел.

2) Множество значений логарифмической функции - множество всех действительных чисел.

3) Логарифмическая функция не является ограниченной.

4) Логарифмическая функция y = log a x является возрастающей на промежутке \((0; +\infty) \), если a > 1,
и убывающей, если 0
5) Если a > 1, то функция y = log a x принимает положительные значения при х > 1,
отрицательные при 0 Если 0 отрицательные при х > 1.

Ось Oy является вертикальной асимптотой графика функции y = log a x

Отметим, что график любой логарифмической функции y = log a x проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:

Теорема. Если log a x 1 = log a x 2 где a > 0, \(a \neq 1 \), x 1 > 0, x 2 > 0, то x 1 = x 2

Логарифмическая функция y = log a x и показательная функция y = a x , где a > 0, \(a \neq 1 \), взаимно обратны.

Логарифмические уравнения

Решить уравнение log 2 (x+1) + log 2 (x+3) = 3
Предположим, что х - такое число, при котором равенство является верным, т.е. х - корень уравнения. Тогда по свойству логарифма верно равенство
log 2 ((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х 2 + 4х + 3 = 8, т.е. х 2 + 4x - 5 = 0, откуда x 1 = 1, х 2 = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
Подставляя в левую часть исходного уравнения х = 1, получаем
log 2 (1+1) + log 2 (1+3) = log 2 2 + log 2 4 = 1 + 2 = 3, т.е. х = 1 - корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т.е. х = -5 не является корнем этого уравнения.
Ответ x = 1

Решить уравнение lg(2x 2 - 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x 2 - 4x + 12) = lg(x 2 + 3x)
откуда
2x 2 - 4x + 12 = x 2 + 3x
x 2 - 7x + 12 = 0
x 1 = 3, х 2 = 4

Ответ x 1 = 3, х 2 = 4

Решить уравнение log 4 (2x - 1) log 4 x = 2 log 4 (2x - 1)
Преобразуем данное уравнение:
log 4 (2x - 1) log 4 x - 2 log 4 (2x - 1) = 0
log 4 (2х - 1) (log 4 x - 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log 4 (2х - 1) = 0, откуда 2х - 1 = 1, х 1 = 1
2) log 4 х - 2 = 0, откуда log 4 = 2, х 2 = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x 1 = 1, х 2 = 16

По мере развития общества, усложнения производства развивалась и математика. Движение от простого к сложному. От обычного учёта методом сложения и вычитания, при их многократном повторении, пришли к понятию умножения и деления. Сокращение многократно повторяемой операции умножения стало понятием возведения в степень. Первые таблицы зависимости чисел от основания и числа возведения в степень были составлены ещё в VIII веке индийским математиком Варасена. С них и можно отсчитывать время возникновения логарифмов.

Исторический очерк

Возрождение Европы в XVI веке стимулировало и развитие механики. Требовался большой объем вычисления , связанных с умножением и делением многозначных чисел. Древние таблицы оказали большую услугу. Они позволяли заменять сложные операции на более простые – сложение и вычитание. Большим шагом вперёд стала работа математика Михаэля Штифеля, опубликованная в 1544 году, в которой он реализовал идею многих математиков. Что позволило использовать таблицы не только для степеней в виде простых чисел, но и для произвольных рациональных.

В 1614 году шотландец Джон Непер, развивая эти идеи, впервые ввёл новый термин «логарифм числа». Были составлены новые сложные таблицы для расчёта логарифмов синусов и косинусов, а также тангенсов. Это сильно сократило труд астрономов.

Стали появляться новые таблицы, которые успешно использовались учёными на протяжении трёх веков. Прошло немало времени, прежде чем новая операция в алгебре приобрела свой законченный вид. Было дано определение логарифма, и его свойства были изучены.

Только в XX веке с появлением калькулятора и компьютера человечество отказалось от древних таблиц, успешно работавших на протяжении XIII веков.

Сегодня мы называем логарифмом b по основанию a число x, которое является степенью числа а, чтобы получилось число b. В виде формулы это записывается: x = log a(b).

Например, log 3(9) будет равен 2. Это очевидно, если следовать определению. Если 3 возвести в степень 2, то получим 9.

Так, сформулированное определение ставит только одно ограничение, числа a и b должны быть вещественными.

Разновидности логарифмов

Классическое определение носит название вещественный логарифм и фактически является решением уравнения a x = b. Вариант a = 1 является пограничным и не представляет интереса. Внимание: 1 в любой степени равно 1.

Вещественное значение логарифма определено только при основании и аргументе больше 0, при этом основание не должно равняться 1.

Особое место в области математики играют логарифмы, которые будут называться в зависимости от величины их основания:

Правила и ограничения

Основополагающим свойством логарифмов является правило: логарифм произведения равен логарифмической сумме. log abp = lоg a(b) + log a(p).

Как вариант этого утверждения будет: log с(b/p) = lоg с(b) — log с(p), функция частного равна разности функций.

Из предыдущих двух правил легко видно, что: lоg a(b p) = p * log a(b).

Среди других свойств можно выделить:

Замечание. Не надо делать распространённую ошибку - логарифм суммы не равен сумме логарифмов.

Многие века операция поиска логарифма была довольно трудоёмкой задачей. Математики пользовались известной формулой логарифмической теории разложения на многочлен:

ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*((x^n)/n), где n - натуральное число больше 1, определяющее точность вычисления.

Логарифмы с другими основаниями вычислялись, используя теорему о переходе от одного основания к другому и свойстве логарифма произведения.

Так как этот способ очень трудоёмкий и при решении практических задач трудноосуществим, то использовали заранее составленные таблицы логарифмов, что значительно ускоряло всю работу.

В некоторых случаях использовали специально составленные графики логарифмов, что давало меньшую точность, но значительно ускоряло поиск нужного значения. Кривая функции y = log a(x), построенная по нескольким точкам, позволяет с помощью обычной линейки находить значения функции в любой другой точке. Инженеры длительное время для этих целей использовали так называемую миллиметровую бумагу.

В XVII веке появились первые вспомогательные аналоговые вычислительные условия, которые к XIX веку приобрели законченный вид. Наиболее удачное устройство получило название логарифмическая линейка. При всей простоте устройства, её появление значительно ускорило процесс всех инженерных расчётов, и это переоценить трудно. В настоящее время уже мало кто знаком с этим устройством.

Появление калькуляторов и компьютеров сделало бессмысленным использование любых других устройств.

Уравнения и неравенства

Для решения различных уравнений и неравенств с использованием логарифмов применяются следующие формулы:

• Переход от одного основания к другому: lоg a(b) = log c(b) / log c(a);
• Как следствие предыдущего варианта: lоg a(b) = 1 / log b(a).

Для решения неравенств полезно знать:

• Значение логарифма будет положительным только в том случае, когда основание и аргумент одновременно больше или меньше единицы; если хотя бы одно условие нарушено, значение логарифма будет отрицательным.
• Если функция логарифма применяется к правой и левой части неравенства, и основание логарифма больше единицы, то знак неравенства сохраняется; в противном случае он меняется.

Примеры задач

Рассмотрим несколько вариантов применения логарифмов и их свойства. Примеры с решением уравнений:

Рассмотрим вариант размещения логарифма в степени:

• Задача 3. Вычислить 25^log 5(3). Решение: в условиях задачи запись аналогична следующей (5^2)^log5(3) или 5^(2 * log 5(3)). Запишем по-другому: 5^log 5(3*2), или квадрат числа в качестве аргумента функции можно записать как квадрат самой функции (5^log 5(3))^2. Используя свойства логарифмов, это выражение равно 3^2. Ответ: в результате вычисления получаем 9.

Практическое применение

Являясь исключительно математическим инструментом, кажется далёким от реальной жизни, что логарифм неожиданно приобрёл большое значение для описания объектов реального мира. Трудно найти науку, где его не применяют. Это в полной мере относится не только к естественным, но и гуманитарным областям знаний.

Логарифмические зависимости

Приведём несколько примеров числовых зависимостей:

Механика и физика

Исторически механика и физика всегда развивались с использованием математических методов исследования и одновременно служили стимулом для развития математики, в том числе логарифмов. Теория большинства законов физики написана языком математики. Приведём только два примера описания физических законов с использованием логарифма.

Решать задачу расчёта такой сложной величины как скорость ракеты можно, применяя формулу Циолковского, которая положила начало теории освоения космоса:

V = I * ln (M1/M2), где

• V – конечная скорость летательного аппарата.
• I – удельный импульс двигателя.
• M 1 – начальная масса ракеты.
• M 2 – конечная масса.

Другой важный пример - это использование в формуле другого великого учёного Макса Планка, которая служит для оценки равновесного состояния в термодинамике.

S = k * ln (Ω), где

• S – термодинамическое свойство.
• k – постоянная Больцмана.
• Ω – статистический вес разных состояний.

Химия

Менее очевидным будет использования формул в химии, содержащих отношение логарифмов. Приведём тоже только два примера:

• Уравнение Нернста, условие окислительно-восстановительного потенциала среды по отношению к активности веществ и константой равновесия.
• Расчёт таких констант, как показатель автопролиза и кислотность раствора тоже не обходятся без нашей функции.

Психология и биология

И уж совсем непонятно при чём здесь психология. Оказывается, сила ощущения хорошо описывается этой функцией как обратное отношение значения интенсивности раздражителя к нижнему значению интенсивности.

После вышеприведённых примеров уже не удивляет, что и в биологии широко используется тема логарифмов. Про биологические формы, соответствующие логарифмическим спиралям, можно писать целые тома.

Другие области

Кажется, невозможно существование мира без связи с этой функцией, и она правит всеми законами. Особенно, когда законы природы связаны с геометрической прогрессией. Стоит обратиться к сайту МатПрофи, и таких примеров найдётся множество в следующих сферах деятельности:

Список может быть бесконечным. Освоив основные закономерности этой функции, можно окунуться в мир бесконечной мудрости.

По основанию числа е : ln x = log e x .

Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/ x .

Исходя из определения , основанием натурального логарифма является число е :
е ≅ 2,718281828459045... ;
.

График функции y = ln x .

График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .

Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма является минус бесконечность ( - ∞ ).

При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a растет быстрее логарифма.

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.

Значения ln x

ln 1 = 0

Основные формулы натуральных логарифмов

Формулы, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:

Доказательства этих формул представлены в разделе "Логарифм" .

Обратная функция

Обратной для натурального логарифма является экспонента .

Если , то

Если , то .

Производная ln x

Производная натурального логарифма:
.
Производная натурального логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Интеграл вычисляется интегрированием по частям :
.
Итак,

Выражения через комплексные числа

Рассмотрим функцию комплексной переменной z :
.
Выразим комплексную переменную z через модуль r и аргумент φ :
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n - целое,
то будет одним и тем же числом при различных n .

Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.